El modelo de circuito de computación

Otro modelo de computación importante en el estudio de la computación cuántica es el de familias uniformes de circuitos reversibles.

Definición y Componentes de los Circuitos

  • Los circuitos son redes compuestas de cables que llevan valores de bits a compuertas que realizan operaciones elementales en los bits.

  • Un circuito CnC_{n} tiene nn cables.

  • Los bits de entrada son escritos en los cables y entran al circuito de izquierda a derecha.

  • En cada paso de tiempo tt, cada cable puede tener a lo más una compuerta.

  • Los bits de salida son las lecturas de los cables al final del circuito.

Familias de Circuitos

  • Una familia de circuitos es un conjunto de circuitos {Cn∣n∈Z+}\{C_{n}|n \in \mathbb{Z^{+}}\}.

  • Se dice que la familia es uniforme si podemos construir fácilmente cada CnC_{n}.

    • "Fácilmente" en este contexto significa que existe un algoritmo eficiente (generalmente en tiempo polinomial) que, dado nn, puede generar la descripción del circuito CnC_{n}.

    • La uniformidad es importante porque garantiza que no estamos "codificando" la solución del problema en la construcción del circuito, sino que estamos realmente computando la solución.

Universalidad en Computación Clásica

Un conjunto de compuertas es universal para la computación clásica si, para cualquier entero positivo nn, mm y una función f:{0,1}n→{0,1}mf:\{0,1\}^{n}\rightarrow\{0,1\}^{m}, un circuito puede ser construido para computar ff usando únicamente compuertas de ese conjunto.

  • El conjunto que comprende solo la compuerta TOFFOLI es universal para la computación clásica.

Máquinas de Turing Probabilísticas vs Deterministas

  • Es una pregunta abierta si una máquina de Turing probabilística es más poderosa que una máquina de Turing determinista.

  • Hay algunos problemas donde no se conoce cómo resolverlos usando una máquina de Turing determinista pero se conoce cómo resolverlos eficientemente usando la máquina probabilística.

Ejemplo: Prueba de primalidad

  • Determinista: El algoritmo AKS (Agrawal-Kayal-Saxena) puede determinar si un número es primo en tiempo polinomial, pero es complejo y relativamente lento en la práctica.

  • Probabilístico: El test de Miller-Rabin puede determinar si un número es compuesto (no primo) con alta probabilidad, y es mucho más rápido en la práctica. Si el test dice que un número es "probablemente primo" muchas veces seguidas, podemos estar muy seguros de que es realmente primo.

Medidas de Complejidad en Circuitos

Para el modelo de circuitos, dos medidas naturales de complejidad son:

  1. El número de compuertas usadas en el circuito CnC_{n}.

    • Esta medida se relaciona con el "tamaño" del circuito y puede compararse con el tiempo de ejecución en otros modelos.

  2. La profundidad del circuito.

    • La profundidad es la longitud del camino más largo desde una entrada hasta una salida en el circuito.

    • Se relaciona con el tiempo que tomaría ejecutar el circuito si las compuertas en diferentes caminos pudieran operar en paralelo.

Formulación del Modelo de Circuitos Usando Álgebra Lineal

Estados en Circuitos Deterministas vs Probabilísticos

  • En un circuito determinista, el estado de un cable en un punto dado es simplemente el valor del bit en ese cable (0 o 1).

  • Para un circuito probabilístico, necesitamos una representación más rica que capture las probabilidades de los diferentes estados posibles.

Representación Vectorial de Estados

Para un bit probabilístico que está en estado 0 con probabilidad p0p_{0} y en estado 1 con probabilidad p1p_{1}, podemos usar un vector 2-dimensional de probabilidades:

(p0p1) \begin{pmatrix} p_{0} \\ p_{1} \end{pmatrix}

  • Un cable en estado determinista 0 se representa como: (10)\begin{pmatrix} 1 \\ 0 \end{pmatrix}

  • Un cable en estado determinista 1 se representa como: (01)\begin{pmatrix} 0 \\ 1 \end{pmatrix}

Representación Matricial de Compuertas

Como se decidió representar los estados con vectores, nos gustaría representar las compuertas en el circuito como operadores que actúan en los estados. Pensando en la compuerta NOT, queremos algo tal que:

NOT(10)=(01) NOT\begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} NOT(01)=(10) NOT\begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}

Por lo que podemos llegar a que

NOT=[0110] NOT= \begin{bmatrix} 0 &1\\ 1 & 0 \end{bmatrix}

Así:

[0110](10)=(01) \begin{bmatrix} 0 &1\\ 1 & 0 \end{bmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}

Circuitos Probabilísticos con Dos Cables:

Imaginemos un circuito electrónico simple con dos cables independientes. En un circuito probabilístico, en lugar de tener estados deterministas (siempre 0 o siempre 1), cada cable tiene una probabilidad asociada a cada estado posible.

Para el primer cable:

  • La probabilidad de estar en estado 0 es p0p_0

  • La probabilidad de estar en estado 1 es p1p_1

Para el segundo cable:

  • La probabilidad de estar en estado 0 es q0q_0

  • La probabilidad de estar en estado 1 es q1q_1

Naturalmente, para cada cable, la suma de las probabilidades debe ser 1: p0+p1=1p_0 + p_1 = 1 y q0+q1=1q_0 + q_1 = 1

Ahora, cuando consideramos ambos cables juntos, tenemos cuatro posibles combinaciones de estados:

  1. 00: Ambos cables en estado 0

  2. 01: Primer cable en 0, segundo en 1

  3. 10: Primer cable en 1, segundo en 0

  4. 11: Ambos cables en estado 1

La probabilidad de cada combinación se calcula multiplicando las probabilidades individuales de cada cable. Esto se debe a que asumimos que los estados de los cables son independientes entre sí. Por ejemplo:

  • P(00)=p0⋅q0P(00) = p_0 \cdot q_0

  • P(01)=p0⋅q1P(01) = p_0 \cdot q_1

  • P(10)=p1⋅q0P(10) = p_1 \cdot q_0

  • P(11)=p1⋅q1P(11) = p_1 \cdot q_1

Estas probabilidades combinadas se pueden representar en un vector 4-dimensional:

(p0q0p0q1p1q0p1q1) \begin{pmatrix} p_{0}q_{0} \\ p_{0}q_{1} \\ p_{1}q_{0} \\ p_{1}q_{1} \end{pmatrix}

Ahora, observamos que este vector 4-dimensional se puede expresar como el producto tensorial de dos vectores 2-dimensionales:

(p0q0p0q1p1q0p1q1)=(p0p1)⊗(q0q1) \begin{pmatrix} p_{0}q_{0} \\ p_{0}q_{1} \\ p_{1}q_{0} \\ p_{1}q_{1} \end{pmatrix} = \begin{pmatrix} p_{0} \\ p_{1} \end{pmatrix} \otimes \begin{pmatrix} q_{0} \\ q_{1} \end{pmatrix}

Podemos ver al producto tensorial como una operación que combina dos espacios vectoriales para formar uno nuevo. En nuestro caso, estamos combinando dos espacios 2-dimensionales para formar uno 4-dimensional.

Ahora, lo que estamos usando aquí es el producto de Kronecker, que es una representación matricial del producto tensorial. Para vectores y matrices finitas, ambos son equivalentes en la práctica. La diferencia principal es que el producto tensorial es un concepto más general que se aplica a espacios vectoriales abstractos, mientras que el producto de Kronecker es una operación específica entre matrices.

Ahora, es importante saber qué también podemos representar compuertas que actúan en más de un cable.

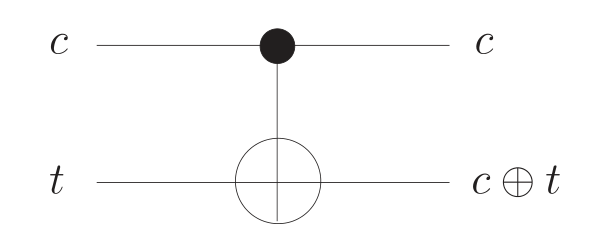
Para eso primero hay que tener claro qué es un bit de control y un bit de objetivo, para eso pensemos en la compuerta CNOT, que tiene la siguiente tabla de verdad:

Control (Qubit 1) Objetivo (Qubit 2) Salida Control Salida Objetivo
0 0 0 0
0 1 0 1
1 0 1 1
1 1 1 0

Entonces aquí un Bit de Control es el qubit que determina si la operación NOT se aplicará al qubit objetivo. Mientras que el Bit de Objetivo es el qubit al que se le aplicará la operación NOT condicionalmente.

Por lo tanto:

  • Si el bit de control es (0), el bit de objetivo no cambia.

  • Si el bit de control es (1), se aplica una operación NOT al bit de objetivo, invirtiendo su valor (de (0) a (1) o de (1) a (0)).

Ahora, aquí en mi clase lo que se procedió fue mostrar cómo se veía esta compuerta en forma matricial de la forma en que se hizo con la compuerta NOT.

Se dijo que:

CNOT=[1000010000010010] \text{CNOT} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ % |00> -> |00> 0 & 1 & 0 & 0 \\ % |01> -> |01> 0 & 0 & 0 & 1 \\ % |10> -> |11> 0 & 0 & 1 & 0 % |11> -> |10> \end{bmatrix}

En su momento no entendí de dónde salía esta representación, así que ya en casita, con la tranquilidad del mundo, llegué al siguiente desarrollo:

Primero recordamos que para este caso, tenemos 2 qubits, en donde tenemos las siguientes combinaciones de estados base: ∣00⟩|00\rangle, ∣01⟩|01\rangle, ∣10⟩|10\rangle, y ∣11⟩|11\rangle.

Pero cuando trabajamos con dos qubits, utilizamos el producto tensorial para combinar los estados de los qubits individuales. Por lo que:

  • ∣00⟩=∣0⟩⊗∣0⟩|00\rangle = |0\rangle \otimes |0\rangle

  • ∣01⟩=∣0⟩⊗∣1⟩|01\rangle = |0\rangle \otimes |1\rangle

  • ∣10⟩=∣1⟩⊗∣0⟩|10\rangle = |1\rangle \otimes |0\rangle

  • ∣11⟩=∣1⟩⊗∣1⟩|11\rangle = |1\rangle \otimes |1\rangle

Para construir estos estados combinados, calculamos el producto tensorial:

  1. Para ∣00⟩|00\rangle:

∣0⟩⊗∣0⟩=[10]⊗[10]=[1×[10]0×[10]]=[1000] |0\rangle \otimes |0\rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 \times \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\ 0 \times \begin{bmatrix} 1 \\ 0 \end{bmatrix} \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}

  1. **Para ∣01⟩|01\rangle:

∣0⟩⊗∣1⟩=[10]⊗[01]=[1×[01]0×[01]]=[0100] |0\rangle \otimes |1\rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \times \begin{bmatrix} 0 \\ 1 \end{bmatrix} \\ 0 \times \begin{bmatrix} 0 \\ 1 \end{bmatrix} \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}

  1. Para ∣10⟩|10\rangle:

∣1⟩⊗∣0⟩=[01]⊗[10]=[0×[10]1×[10]]=[0010] |1\rangle \otimes |0\rangle = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \otimes \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \times \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\ 1 \times \begin{bmatrix} 1 \\ 0 \end{bmatrix} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix}

  1. Para ∣11⟩|11\rangle:

∣1⟩⊗∣1⟩=[01]⊗[01]=[0×[01]1×[01]]=[0001] |1\rangle \otimes |1\rangle = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \times \begin{bmatrix} 0 \\ 1 \end{bmatrix} \\ 1 \times \begin{bmatrix} 0 \\ 1 \end{bmatrix} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}

  • Para ∣00⟩|00\rangle: La compuerta CNOT no cambia nada (porque el control es (00), por lo que ∣00⟩|00\rangle sigue siendo ∣00⟩|00\rangle. Así, la columna correspondiente a ∣00⟩|00\rangle es [1000]\begin{bmatrix}1 \\ 0 \\ 0 \\ 0\end{bmatrix}.

  • Para ∣01⟩|01\rangle: Similar al anterior, el control es (00), así que ∣01⟩|01\rangle sigue siendo ∣01⟩|01\rangle. La columna correspondiente es [0100]\begin{bmatrix}0 \\ 1 \\ 0 \\ 0\end{bmatrix}.

  • Para ∣10⟩|10\rangle: Aquí, el control es (11), así que la compuerta CNOT aplica un NOT al objetivo, transformando ∣10⟩|10\rangle en ∣11⟩|11\rangle. Por lo tanto, la columna correspondiente a ∣10⟩|10\rangle es [0001]\begin{bmatrix}0 \\ 0 \\ 0 \\ 1\end{bmatrix}.

  • Para ∣11⟩|11\rangle: Con el control en (1)(1), la compuerta CNOT cambia el estado del objetivo: ∣11⟩|11\rangle se convierte en ∣10⟩|10\rangle. La columna correspondiente es [0010]\begin{bmatrix}0 \\ 0 \\ 1 \\ 0\end{bmatrix}.

Juntando los resultados ahora llegamos a que:

CNOT=[1000010000010010] \text{CNOT} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix}

Definitivamente esta talachita puede ser excesiva, supongo que con algo más de callo, puede salir a ojo. Pero creo que justamente necesitaba ver este desarrollo para sentirme seguro.

Nota final: En la compuerta CNOT, cuando aplicamos la operación al qubit de objetivo tt en función del qubit de control cc, la operación realizada sobre el qubit de objetivo puede describirse como una suma módulo 2 o suma XOR.

Esta suma módulo 2 es una operación que es como una suma usual pero con la particularidad de que los resultados se reducen al módulo 2. Esto es como la operación XOR. Los resultados de la suma módulo 2 son:

0+0=0(moˊdulo 2)0+1=1(moˊdulo 2)1+0=1(moˊdulo 2)1+1=0(moˊdulo 2) \begin{align*} 0 + 0 & = 0 \quad (\text{módulo } 2) \\ 0 + 1 & = 1 \quad (\text{módulo } 2) \\ 1 + 0 & = 1 \quad (\text{módulo } 2) \\ 1 + 1 & = 0 \quad (\text{módulo } 2) \end{align*}

Por lo que en la compuerta CNOT, la salida del qubit objetivo t′t' se obtiene mediante:

t′=c⊕t t' = c \oplus t

jet2