Un poquito de cuántica nomás para recordar

Aquí se dijo un poco de todo, así que seguiré con esta especie de hacer mis notas con base a enunciados que consider importantes, y solo siendo más detallado en algunos.

• Primer postulado: El estado de un sistema está descrito por un vector unitario en un espacio de Hilbert $\mathcal{H}$.

• La dimensionalidad de H depende de los grados de libertad del sistema, es decir, de las posibles configuraciones o estados que el sistema puede tener.

• Para algunos sistemas, como la posición de una partícula en un espacio continuo, el espacio de Hilbert puede ser de dimensión infinita.

• En la computación cuántica práctica, generalmente se utilizan espacios de dimensión finita.

• Al tener recursos finitos, no podemos distinguir verdaderamente entre un espacio continuo y uno que esté muy discretizado.

La computación cuántica se enfoca en sistemas que están compuestos por múltiples subsistemas de dos niveles, conocidos como qubits. Un sistema de dos niveles es un sistema cuántico que puede existir en dos estados de energía distintos y discretos. Estos sistemas son fundamentales porque representan la unidad básica de información en la computación cuántica, análoga al bit en la computación clásica.

Ejemplos comunes de sistemas de dos niveles incluyen:

• Espín de Electrones: Un electrón tiene espín-1/2, lo que significa que puede estar en uno de dos estados de espín: "espín arriba" ($\ket{\uparrow}$) o "espín abajo" ($\ket{\downarrow}$).

• Polarización de Fotones: Los fotones pueden tener polarización horizontal ($\ket{H}$) o vertical ($\ket{V}$).

• Estados Electrónicos en Átomos: Un átomo puede estar en su estado fundamental o en un estado excitado específico.

Estos sistemas se describen matemáticamente mediante vectores en un espacio de Hilbert de dos dimensiones. Este espacio es un marco matemático que permite representar y manipular estados cuánticos utilizando técnicas algebraicas y geométricas.

Representación de Qubits y la Base Computacional

Un qubit es la unidad básica de información en la computación cuántica y se representa como un vector en un espacio de Hilbert bidimensional. Para manipular y entender estos qubits, elegimos una base ortonormal, comúnmente denotada como $\ket{0}$ y $\ket{1}$. Esta base se conoce como la base computacional y es análoga a los estados 0 y 1 en la computación clásica.

A diferencia de los bits clásicos, que solo pueden estar en uno de los dos estados, un qubit puede estar en cualquier superposición de los estados base:

$$\ket{\psi} = \alpha_0 \ket{0} + \alpha_1 \ket{1}$$

donde $\alpha_0$ y $\alpha_1$ son amplitudes de probabilidad complejas que determinan la probabilidad y la fase asociada a cada estado.

Amplitudes Complejas y Fases

Las amplitudes $\alpha_0$ y $\alpha_1$ son números complejos que pueden expresarse en términos de su módulo y fase:

$$\alpha = |\alpha| e^{i\theta}$$

• $|\alpha|$ es el módulo de la amplitud y representa la probabilidad de encontrar el qubit en ese estado después de una medición.

• $e^{i\theta}$ es el factor de fase, donde $\theta$ es la fase asociada.

Esta descomposición es única debido a la naturaleza de los números complejos en forma polar: cada número complejo tiene una representación única en términos de su magnitud positiva y su ángulo (fase) entre 0 y $2\pi$.

Para que el estado $\ket{\psi}$ esté normalizado, es decir, que la suma de las probabilidades sea 1, las amplitudes deben satisfacer:

$$|\alpha_0|^2 + |\alpha_1|^2 = 1$$

Esto garantiza que al medir el qubit, siempre obtendremos un resultado válido dentro del espacio de estados posibles.

El Espín y Sistemas de Dos Niveles en la Cuántica

El espín es una propiedad intrínseca de las partículas cuánticas sin un análogo directo en la física clásica. Para partículas con espín-1/2, como los electrones, existen dos estados de espín posibles:

• Espín Arriba ($\ket{\uparrow}$ o $\ket{0}$): Representa un estado de espín en una dirección específica.

• Espín Abajo ($\ket{\downarrow}$ o $\ket{1}$): Representa el estado opuesto.

Aunque los electrones pueden ocupar infinitos niveles de energía, en muchos casos prácticos nos enfocamos en solo dos niveles energéticos relevantes, como el estado fundamental y un estado excitado específico. Esta simplificación nos permite modelar el sistema como un qubit y aplicar las técnicas de la computación cuántica.

Fase Global vs. Fase Relativa

En mecánica cuántica, los estados que difieren solo por un factor de fase global $e^{i\theta}$ son físicamente equivalentes. Es decir:

$$\ket{\psi} \quad \text{y} \quad e^{i\theta}\ket{\psi}$$

representan el mismo estado físico, ya que las observables (como probabilidades y valores esperados) dependen de las fases relativas entre los estados, no de la fase global.

Por ejemplo, el estado:

$$\ket{\psi} = \ket{0} + \ket{1}$$

es físicamente equivalente a:

$$\ket{\psi'} = e^{i\theta}(\ket{0} + \ket{1})$$

Sin embargo, la fase relativa entre los componentes de la superposición es crucial. El estado:

$$\ket{\psi} = \ket{0} + \ket{1}$$

es físicamente diferente de:

$$\ket{\phi} = \ket{0} + e^{i\phi}\ket{1}$$

cuando $\phi \neq 0$, ya que esta fase relativa afecta los patrones de interferencia y, por ende, los resultados de mediciones.

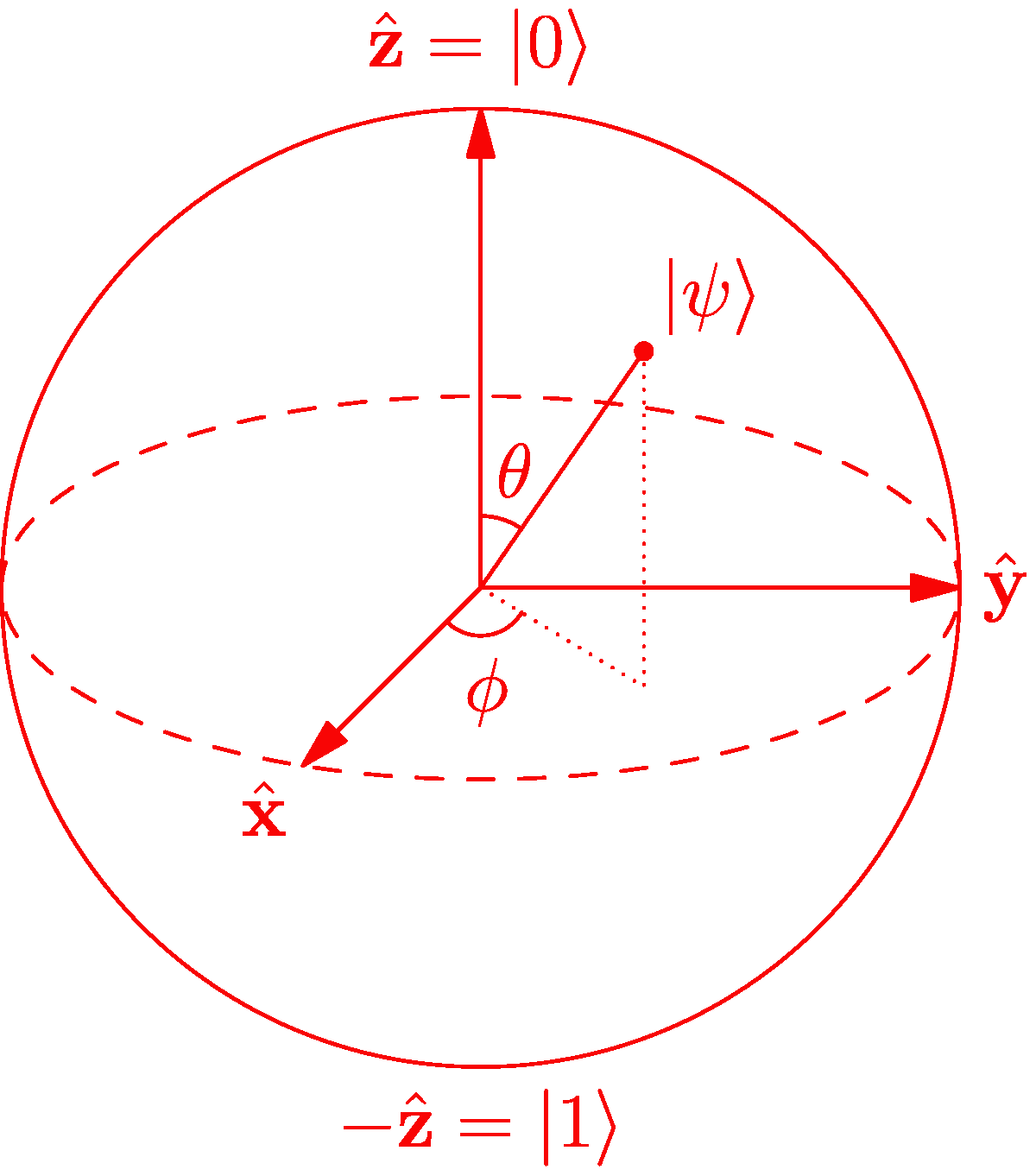
Representación General de un Qubit

El estado más general de un qubit, eliminando la fase global y asegurando la normalización, se puede escribir como:

$$\ket{\psi} = \cos\left(\frac{\theta}{2}\right)\ket{0} + e^{i\phi}\sin\left(\frac{\theta}{2}\right)\ket{1}$$

Los números $0 \leq θ \leq \pi$ y $0 \leq \phi \leq 2\pi$ definen un punto en una esfera unitaria de tres dimensiones. Esta es la esfera de Bloch. Siempre vale la pena ver la derivación de esta expresión, hay muchos recursos en internet donde hacen esto, yo la vi aquí.

Comparación entre Bits Clásicos y Qubits

• Bit Clásico:

  • Solo puede estar en uno de dos estados discretos: 0 o 1.

  • No admite superposición ni fases.

• Bit Clásico Probabilístico:

  • Puede representarse mediante una distribución de probabilidad entre 0 y 1.

  • Tiene un continuo unidimensional de estados posibles (segmento de línea entre 0 y 1).

• Qubit:

  • Puede estar en cualquier superposición coherente de $\ket{0}$ y $\ket{1}$.

  • Posee un continuo bidimensional de estados (superficie de una esfera), incorporando tanto amplitudes como fases relativas.

  • Ofrece capacidades como la superposición y el entrelazamiento, que no tienen equivalentes clásicos.

Evolución temporal de un sistema cerrado

• Un sistema físico cambia con el tiempo, por lo que, en realidad el vector de estado $\ket{\psi}$ es una función del tiempo $\ket{\psi(t)}$.

• Linealidad de la evolución cuántica: La teoría cuántica establece que la evolución temporal de un estado en un sistema cerrado es lineal. Esto significa que si un sistema puede estar en los estados $\ket{\psi_1}$ y $\ket{\psi_2}$, entonces cualquier superposición lineal de estos estados también evolucionará de manera lineal en el tiempo.

  Ejemplo: Si consideramos un sistema en una superposición de estados $\ket{\psi(t)} = \alpha \ket{\psi_1(t)} + \beta \ket{\psi_2(t)}$, donde $\alpha$ y $\beta$ son coeficientes complejos, la evolución temporal preservará esta superposición lineal, es decir, cada componente evoluciona independientemente.

• Normalización del vector de estado: Los coeficientes $\alpha_i$ de un vector de estado deben cumplir la condición de normalización:

$$\sum_{i}|\alpha_{i}|^{2}=1.$$

Esto asegura que la probabilidad total de encontrar el sistema en alguno de los estados posibles es uno.

Postulado de evolución: La evolución temporal de un estado en un sistema cuántico cerrado está descrita por un operador unitario. Por lo que, para cualquier evolución existe un operador unitario $U$ tal que si el estado inicial del sistema es $\ket{\psi_{1}}$, entonces después de la evolución, el estado del sistema será $\ket{\psi_{2}}=U\ket{\psi_{1}}$.

• Sabemos bien qué onda con un operador lineal cuando lo aplicamos a una base. Podemos representar operadores 2-dimensionales que actúan en un único qubit como matrices de $2\times 2$.

• Por ejemplo, recordamos que la compuerta NOT se representa como

$$NOT= \begin{bmatrix} 0 &1\\ 1 & 0 \end{bmatrix}$$

• En esta entrada recordamos cómo podemos obtener la forma matricial de un operador que actúa en 2 qubits, es decir la compuerta CNOT, y vemos cómo aplicando la compuerta a la base nos permitía obtener la forma matricial.

• Matrices de Pauli: La compuerta NOT se identifica a menudo con el símbolo $X$, una de las matrices de Pauli. Las cuatro matrices de Pauli son fundamentales en la mecánica cuántica y se definen como:

$$\begin{align*} I &= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, \quad X = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}, \\ Y &= \begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}, \quad Z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}. \end{align*}$$

Estas matrices son operadores hermitianos y unitarios que generan el espacio de todos los operadores lineales en un qubit.

Explicación y relación con la negación:

• $X$ (sigma-x): Representa la compuerta NOT cuántica, ya que intercambia los estados $\ket{0}$ y $\ket{1}$.

• $Y$ (sigma-y): Realiza una rotación en el plano complejo, combinando un intercambio de estados con un factor de fase.

• $Z$ (sigma-z): Cambia la fase del estado $\ket{1}$, dejando $\ket{0}$ inalterado.

Estas matrices están relacionadas con las rotaciones en el espacio de estados de un qubit y son fundamentales para describir operaciones cuánticas.

• Relación con la esfera de Bloch: Las matrices de Pauli $X$, $Y$, $Z$ corresponden a rotaciones alrededor de los ejes $x$, $y$ y $z$ de la esfera de Bloch, una representación geométrica del estado de un qubit. En esta esfera, los estados puros de un qubit corresponden a puntos en la superficie, y las rotaciones unitarias se visualizan como rotaciones de estos puntos alrededor de los ejes.

• Relación con el spin: Las matrices de Pauli también están directamente relacionadas con los operadores de spin para partículas con spin 1/2, como los electrones. Los componentes del spin en las direcciones $x$, $y$ y $z$ se representan mediante estas matrices multiplicadas por $\hbar/2$.

• Generación del espacio de operadores de 1-qubit: Las matrices de Pauli, junto con el operador identidad $I$, generan el espacio vectorial de todos los operadores lineales en un qubit. Cualquier operador puede expresarse como una combinación lineal de $I$, $X$, $Y$ y $Z$.

• El carácter unitario de la evolución cuántica implica que es reversible. Esto es una consecuencia directa de tratar con sistemas cerrados donde no hay interacción con el entorno. La reversibilidad es una propiedad esencial en la computación cuántica, ya que las operaciones deben ser unitarias.

• En computación clásica cualquier cómputo irreversible puede ser simulado eficientemente por cómputos clásicos reversibles. Esto también pasa en computación cuántica.

• En cuántica se ve que la evolución temporal continua de un sistema cuántico cerrado, ignorando a la relatividad como siempre, sigue la ecuación de Schrodinger

$$i\hbar \frac{d\ket{\psi(t)} }{dt} = H(t)\ket{\psi(t)}$$

• $H$ es el hamiltoniano, un operador que representa la función de energía total del sistema.

• Hamiltonianos independientes del tiempo: En general, los Hamiltonianos pueden depender del tiempo. Sin embargo, es común considerar Hamiltonianos constantes en el tiempo para simplificar el análisis. Estos sistemas se denominan sistemas cuánticos estacionarios.

• En esos casos, la solución está dada por

$$\ket{\psi(t_{2})} = e^{-i\hbar H(t_{2}-t_{1})}\ket{\psi(t_{1})}$$

Sistemas compuestos

Hasta ahora, hemos discutido los postulados para sistemas individuales, en particular de un qubit. Sin embargo, en muchos casos, necesitamos considerar sistemas compuestos de varios qubits que pueden interactuar entre sí. Es fundamental entender cómo describir el estado de un sistema compuesto, cómo evoluciona en el tiempo y qué ocurre al medirlo.

• Tercer postulado de la mecánica cuántica: Cuando dos sistemas físicos se consideran como un único sistema combinado, el espacio de estados del sistema combinado es el producto tensorial de los espacios de estados individuales. Es decir:

$$\mathcal{H}_{\text{total}} = \mathcal{H}_{1} \otimes \mathcal{H}_{2}.$$

Si el sistema 1 está en el estado $\ket{\psi_{1}}$ y el sistema 2 en el estado $\ket{\psi_{2}}$, el estado del sistema combinado es:

$$\ket{\psi_{\text{total}}} = \ket{\psi_{1}} \otimes \ket{\psi_{2}} = \ket{\psi_{1}\psi_{2}}.$$

• Es análogo generalizar espacios de estado con $n$ subsistemas.

• Es importante notar que no todo estado de un sistema compuesto de 2-qubits puede ser escrito en la forma del producto tensorial.

• Si los dos qubits son preparados independientemente, se mantienen aislados, entonces cada qubit es un sistema cerrado, por lo que el estado puede escribirse como un producto.

• Pero si los qubits pueden interactuar, entonces el sistema cerrado incluye a ambos qubits, y no puede ser posible representar el estado como un producto.

• Cuando lo anterior pasa, se dice que los qubits están entrelazados.

• Si tenemos un sistema compuesto de 2-qubits, y aplicamos la compuerta $X$ al primer qubit, implícitamente estamos aplicando el operador identidad $I$ al segundo qubit.

• $X\ket{\psi_{1}} \otimes I\ket{\psi_{2}}= (X \otimes I)(\ket{\psi_{1}} \otimes \ket{\psi_{2}})$

• Por lo que el operador lineal que describe el aplicarle la compuerta $X$ al primer qubit es $(X \otimes I)$.

• En forma matricial tendríamos

$$\begin{bmatrix} 0 &1\\ 1 & 0 \end{bmatrix} \otimes \begin{bmatrix} 1 &0\\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 0 &0&1&0\\ 0 & 0&0&1 \\ 1&0&0&0 \\ 0&1&0&0 \end{bmatrix}$$

• Si nuestro sistema fuera la composición de $n$ qubits, entonces aplicar $X$ al primer qubit corresponde a aplicar la operación $X \otimes I \otimes I \otimes I \otimes \dots \otimes I$.

• Así como hay estados de 2-qubits que no pueden ser escritos como el producto de dos estados de 1-qubit, también hay compuertas de 2-qubits (actuando de manera no trivial en ambos) que no pueden ser escritas como el producto tensorial de dos compuertas de 1-qubit.

• Un ejemplo es la compuerta CNOT.