Transporte de Jets

Como se ha explorado en otras entradas, tenemos interés en resolver sistemas de ecuaciones diferenciales del tipo:

$$\mathbf{\dot{x}} = f(\mathbf{x}(t), t)$$

Sabemos bien que encontrar soluciones analíticas además de que puede ser un dolor de cabeza, no siempre es posible, por eso es que se recurre a métodos numéricos. Cuando resolvemos el sistema, necesitamos un conjunto $\mathbf{x_0}$ de condiciones iniciales para obtener una solución $\phi(t; t_0, \mathbf{x_0})$ bien caracterizada, si nuestro sistema es una única ecuación diferencial, solo necesitamos una condición inicial, si son dos ecuaciones, dos condiciones iniciales, y así sucesivamente.

Ahora, hay situaciones en nuestro estudio de sistemas dinámicos en que no solo nos interesa resolver para una cierta condición inicial, muchas veces resulta interesante saber qué pasa con la dinámica en regiones cercanas a esta condición inicial.

Esto puede sonar familiar, pues si pensamos en el caso en que no conocemos la condición inicial para una solución conocida, pero sí conocemos el conjunto de todas las condiciones iniciales posibles, podríamos resolver para cada una de ellas y así obtener todas las soluciones, esto en esencia es lo que se hace con los métodos Monte Carlo.

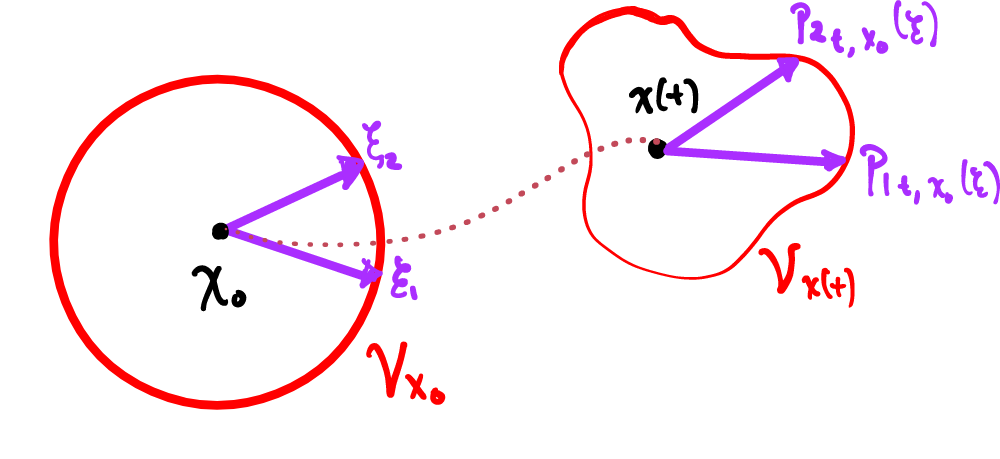
Lo que ahora cambia, con el método de Jet Transport, es que en lugar de obtener las soluciones $\phi(t; t_0, \mathbf{x_0})$, para un $\mathbf{x_0}$, tenemos una vecindad inicial $\mathcal{V}_{\mathbf{x}_0}$, alrededor de $\mathbf{x_0}$. Al resolver, lo que haríamos sería encontrar el flujo para toda esta vecindad, lo que estamos haciendo es tomar un jet y transportarlo por el flujo.

La primera diferencia con la que nos encontramos es que en el caso de los métodos Monte Carlo, se tenía que resolver de manera independiente para cada condición inicial de nuestro conjunto de condiciones iniciales, en el caso de Jet Transport se resuelve para toda la vecindad en una integración.

Por lo que, en lugar de obtener $\phi(t; t_0, \mathbf{x_0})$, tendríamos $\phi(t; t_0, \mathcal{V}_{\mathbf{x_0}})$, que nos diría cómo se va deformando la vecindad de condiciones iniciales con el tiempo.

Para observar un poco más a profundidad este método, como en todo, siempre ayuda pensar en el caso más sencillo. Por definición de derivada, sabemos que:

$$\dot{\mathbf{x}}(t) = \lim_{h \to 0} \frac{\mathbf{x}(t+h) - \mathbf{x}(t)}{h}$$

Si tomamos una $h$ pequeña, entonces podemos aproximar tal que:

$$\dot{\mathbf{x}}(t) \approx \frac{\mathbf{x}(t+h) - \mathbf{x}(t)}{h} \implies \mathbf{x}(t+h) \approx \mathbf{x}(t) + h\dot{\mathbf{x}}(t)$$

en donde recordamos que $\mathbf{\dot{x}} = f(\mathbf{x}(t), t)$ y pensamos en $h$ como un paso de integración tendríamos:

$$\mathbf{x}_{n+1} = \mathbf{x}_{n} + hf(\mathbf{x_n}, t_n)$$

este procedimiento es bien conocido, es el Método de Euler.

Sabemos que nuestra condición inicial es tal que $\mathbf{x_0} \in \mathbb{R}^n$, para parametrizar nuestra vecindad $\mathcal{V}_{\mathbf{x}_0}$ usamos un polinomio $\mathcal{P}_{t_0, \mathbf{x_0}}(\xi)$ alrededor de nuestra condición inicial, para ser más claros, veamos que:

$$\mathcal{P}_{t_0, \mathbf{x_0}}(\xi) = \mathbf{x_0} + \xi = \mathbf{x_0} + (\xi_1, \xi_2, ..., \xi_n)^T$$

Podemos usar el método de Euler y así obtener el flujo de $\mathcal{V}_{\mathbf{x}_0}$ de la forma: $\phi(t; t_0, \mathcal{V}_{\mathbf{x_0}})$, entonces por Euler recordamos que $\mathbf{x}_{n+1} = \mathbf{x}_{n} + hf(\mathbf{x_n}, t_n)$. Por lo tanto:

$$P_{1, x_0}(\xi) := P_{t_0+h, x_0}(\xi) = P_{t_0, x_0}(\xi) + h f(P_{t_0, x_0}, t_0) = x_0 + \xi + h f(x_0 + \xi)$$

Podemos extender la evolución tal que:

$$P_{t_n, x_0}(\xi) = P_{n, x_0}(\xi) = P_{n-1, x_0}(\xi) + h f(P_{n-1, x_0}(\xi), t_{n-1})$$

Evaluando este polinomio en $\mathcal{V}_{x_0}$ permite obtener $\phi(t; t_0, \mathcal{V}_{\mathbf{x_0}})$.

Para ver un poco de este procedimiento en acción, pensemos en uno de nuestros sistemas favoritos, el oscilador armónico.

Vayamos a Julia e importemos las siguientes bibliotecas:

using TaylorIntegration, Plots

Definimos nuestro sistema de la siguiente forma:

function harmonic(du, u, p, t)
    du[1] = u[2]
    du[2] = -u[1]
end

Ahora, primero resolvamos el sistema como lo haríamos normalmente, como el nombre de la paquetería lo dice, usaremos un integrador que usa el método de Taylor. Entonces, necesitamos una condición inicial, un span de tiempo, y como estamos usando el método de Taylor, necesitamos especificar hasta que orden se hará la integración, además incluiremos una tolerancia.

u₀ = [0.0, 1.0] # condición inicial primaria, posición en 0.0, velocidad inicial de 1.0

t0 = 0.0  # tiempo inicial
tf = 2π # tiempo final
step = 0.1 # paso de tiempo
time_vector = t0:step:tf
order = 15 
abstol = 1e-20

Para resolver hacemos:

solution = taylorinteg(harmonic, u₀, time_vector, order, abstol, maxsteps=5000)

Y como era de esperarse, tenemos 63 resultados, uno para cada paso de tiempo, y dos columnas, una correspondiente a nuestras posiciones y otra a nuestras velocidades.

63×2 transpose(::Matrix{Float64}) with eltype Float64:
  0.0        1.0
  0.0998334  0.995004
  0.198669   0.980067
  0.29552    0.955336
  0.389418   0.921061
  0.479426   0.877583
  0.564642   0.825336
  0.644218   0.764842
  0.717356   0.696707
  0.783327   0.62161
  ⋮          
 -0.772764   0.634693
 -0.70554    0.70867
 -0.631267   0.775566
 -0.550686   0.834713
 -0.464602   0.88552
 -0.373877   0.927478
 -0.279415   0.96017
 -0.182163   0.983268
 -0.0830894  0.996542

Si ahora ploteamos el espacio-fase de nuestro sistema:

scatter(solution[:,1], solution[:,2], color=:black, alpha = 0.7, aspect_ratio=:equal)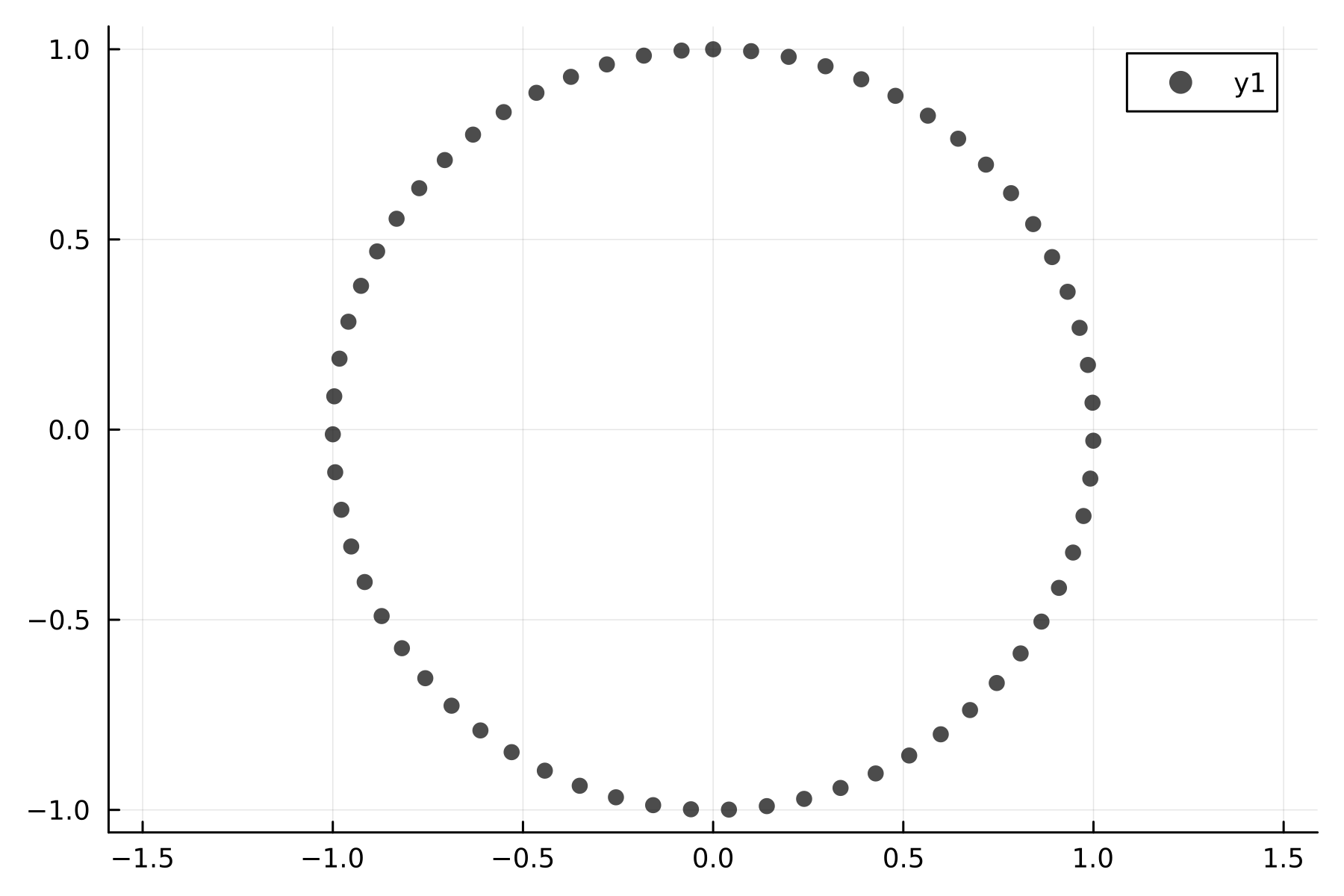

Y bueno, este resultado es bien conocido, aunque el oscilador armónico es muy importante, es cierto que muchas veces ya nos resulta aburrido. Pero continuando con lo que nos importa, lo que ahora nos interesa es hacer un Transporte de Jet. Como dijimos, ahora no nos importa resolver para una única condición inicial, nos interesa parametrizar una vecindad de condiciones iniciales alrededor de alguna condición inicial dada usando un polinomio, entonces:

Recordando que $\mathcal{P}_{t_0, \mathbf{x_0}}(\xi) = \mathbf{x_0} + \xi = \mathbf{x_0} + (\xi_1, \xi_2, ..., \xi_n)^T$

varorder = 13 # el orden de nuestro polinomio

ξ = set_variables("ξ", numvars=2, order=varorder) # dos variables porque nuestra condición inicial es de dos elementos

q0TN = u₀ .+ ξ

2-element Vector{TaylorN{Float64}}:
        1.0 ξ₁ + 𝒪(‖x‖¹⁴)
  1.0 + 1.0 ξ₂ + 𝒪(‖x‖¹⁴)

Ahora volvemos a resolver de la misma forma, pero usando nuestra nueva condición inicial:

result = taylorinteg(harmonic, q0TN, time_vector, order, abstol, maxsteps=5000)

63×2 transpose(::Matrix{TaylorN{Float64}}) with eltype TaylorN{Float64}:
                                                                  1.0 ξ₁ + 𝒪(‖x‖¹⁴)  …                                                          1.0 + 1.0 ξ₂ + 𝒪(‖x‖¹⁴)
    0.09983341664682815 + 0.9950041652780257 ξ₁ + 0.09983341664682815 ξ₂ + 𝒪(‖x‖¹⁴)      0.9950041652780257 - 0.09983341664682815 ξ₁ + 0.9950041652780257 ξ₂ + 𝒪(‖x‖¹⁴)
    0.19866933079506122 + 0.9800665778412416 ξ₁ + 0.19866933079506122 ξ₂ + 𝒪(‖x‖¹⁴)      0.9800665778412416 - 0.19866933079506122 ξ₁ + 0.9800665778412416 ξ₂ + 𝒪(‖x‖¹⁴)
                                                                                  ⋮  ⋱  
    - 0.7727644875559874 + 0.6346928759426342 ξ₁ - 0.7727644875559874 ξ₂ + 𝒪(‖x‖¹⁴)       0.6346928759426342 + 0.7727644875559874 ξ₁ + 0.6346928759426342 ξ₂ + 𝒪(‖x‖¹⁴)
    - 0.7055403255703925 + 0.7086697742912593 ξ₁ - 0.7055403255703925 ξ₂ + 𝒪(‖x‖¹⁴)  …    0.7086697742912593 + 0.7055403255703925 ξ₁ + 0.7086697742912593 ξ₂ + 𝒪(‖x‖¹⁴)

Como podemos ver, ahora en lugar de tener 63 resultados exactos, tenemos 63 polinomios, uno para cada tiempo, de nuevo dos columnas, correspondientes a las posiciones y las velocidades.

Finalmente lo que haría falta sería evaluar cada polinomio en $\mathcal{V}_{x_0}$ para obtener $\phi(t; t_0, \mathcal{V}_{\mathbf{x_0}})$.

Hay muchas formas de parametrizar nuestra vecindad, recordemos que lo que queremos hacer es ver qué pasa cerca de la condición inicial que ya dimos. Podríamos pensar en una "cajita" de condiciones iniciales cercanas nuestra primer condición inicial. Y entonces, lo emocionante sería ver cómo es que esta "cajita" evoluciona con el tiempo. Así, en lugar de ver cómo evoluciona el sistema dada una única condición inicial, ahora tenemos una herramienta más rica.

polar2cart(r, ϕ) = [r*cos(ϕ), r*sin(ϕ)] # covertimos el radio r y el ángulo ϕ a coordenadas cartesianas 

r = 0.05 # el radio de la vecindad

ϕ = 0.0:0.1:(2π+0.1) # valores del ángulo

ξv = polar2cart.(r, ϕ)

64-element Vector{Vector{Float64}}:
 [0.05, 0.0]
 [0.049750208263901294, 0.004991670832341408]
 [0.04900332889206208, 0.009933466539753062]
 [0.047766824456280305, 0.014776010333066981]
 [0.04605304970014426, 0.01947091711543253]
 [0.04387912809451864, 0.02397127693021015]
 [0.041266780745483914, 0.028232123669751776]
 [0.038242109364224425, 0.03221088436188456]
 [0.03483533546735827, 0.035867804544976144]
 [0.03108049841353322, 0.039166345481374175]
 ⋮
 [0.035433488714563, -0.0352770162785196]
 [0.03877829392551251, -0.03156333189361604]
 [0.04173563924195799, -0.02753427712988188]
 [0.04427597584706597, -0.02323010897068783]
 [0.046373921537201795, -0.0186938332415118]
 [0.0480085143325183, -0.013970774909946294]
 [0.04916342192212924, -0.009108125213604752]
 [0.049827104851160875, -0.00415447014087482]
 [0.049992931819170756, 0.0008406950242175301]

Como podemos ver, ahora tenemos una colección de 64 condiciones iniciales alrededor de un punto.

Lo que sigue ahora, es evaluar cada una de estas condiciones iniciales en cada uno de los polinomios que obtuvimos anteriormente.

Antes de proceder, pensemos, teníamos por cada columna 63 polinomios, lo que queremos es, tomar el primer polinomio y evaluarlo en cada una de las 64 condiciones iniciales. Por lo que esperamos 63 resultados, donde cada resultado contiene 64 elementos.

Para evaluar un polinomio lo hacemos de la siguiente forma: Supongamos que elegimos el tercer polinomio de la primera columna

result[3,1]

0.19866933079506122 + 0.9800665778412416 ξ₁ + 0.19866933079506122 ξ₂ + 𝒪(‖x‖¹⁴)

Para evaluarlo, por ejemplo en el segundo punto de ξv bastaría hacer:

result[3,1].([ [0.049750208263901294, 0.004991670832341408]])

1-element Vector{Float64}:
 0.24841953905896252

Entonces, para evaluar todos de una vez, hacemos:

xjet_plot2 = map(λ->λ.(ξv), result[:,1])

vjet_plot2 = map(λ->λ.(ξv), result[:,2])

Sabemos que result es una matriz de $63\times2$, y estamos seleccionando toda la primera columna de esta matriz. El : indica "todas las filas", y el 1 indica "la primera columna".

Cuando hacemos λ->λ.(ξv) es porque estamos usando una función anónima.

• λ es el parámetro de la función.

• λ.(ξv) es el cuerpo de la función. Está aplicando la función λ a cada elemento de ξv usando la sintaxis de "broadcast" (el punto antes del paréntesis).

Finalmente map(función, colección), lo que hace es aplicar la función dada (el primer argumento) a cada elemento de la colección (el segundo argumento). En resumen, lo que hace es:

• Para cada elemento λ en result[:,1]:

• Aplica λ a cada elemento de ξv

• Guarda el resultado en un nuevo array que llamamos xjet_plot2.

63-element Vector{Vector{Float64}}:
 [1.0, 1.0049916708323414, 1.009933466539753, 1.014776010333067, 1.0194709171154326, 1.02397127693021, 1.0282321236697518, 1.0322108843618845, 1.035867804544976, 1.0391663454813742  …  0.9613617756222006, 0.9647229837214804, 0.968436668106384, 0.9724657228701181, 0.9767698910293122, 0.9813061667584883, 0.9860292250900538, 0.9908918747863953, 0.9958455298591252, 1.0008406950242175]
 [0.9900124944456843, 0.9950041652780257, 0.9999958361103671, 1.0049376318177787, 1.0097801756110927, 1.0144750823934583, 1.0189754422082358, 1.0232362889477775, 1.0272150496399102, 1.0308719698230018  …  0.9533907931668306, 0.9563659409002263, 0.9597271489995062, 0.9634408333844097, 0.9674698881481438, 0.9717740563073378, 0.9763103320365139, 0.9810333903680795, 0.985896040064421, 0.9908496951371509]
 ⋮
 [0.6733311003204336, 0.6763062480538293, 0.6788656087286419, 0.6809836100590209, 0.6826390896757911, 0.6838155065738508, 0.6845011063844263, 0.6846890388208393, 0.6843774261243074, 0.6835693818258891  …  0.6346928759426342, 0.6396845467749757, 0.6446263424823874, 0.6494688862757012, 0.6541637930580668, 0.6586641528728444, 0.662924999612386, 0.6669037603045188, 0.6705606804876104, 0.6738592214240084]
 [0.743946790569779, 0.7473079986690587, 0.7502831464024544, 0.752842507077267, 0.754960508407646, 0.7566159880244163, 0.757792404922476, 0.7584780047330514, 0.7586659371694644, 0.7583543244729325  …  0.703678103458918, 0.7086697742912593, 0.7136614451236009, 0.7186032408310125, 0.7234457846243264, 0.7281406914066919, 0.7326410512214695, 0.7369018979610111, 0.7408806586531439, 0.7445375788362355]

Como era de esperar, tenemos 63 resultados, y en cada resultado, hay 64 elementos.

Entonces, ahora, graficando nuestros resultados, tendríamos que:

begin
    plot!(xjet_plot2, vjet_plot2, legend=false)
    scatter!(solution[:,1], solution[:,2], color=:black, alpha = 0.7, aspect_ratio=:equal)
end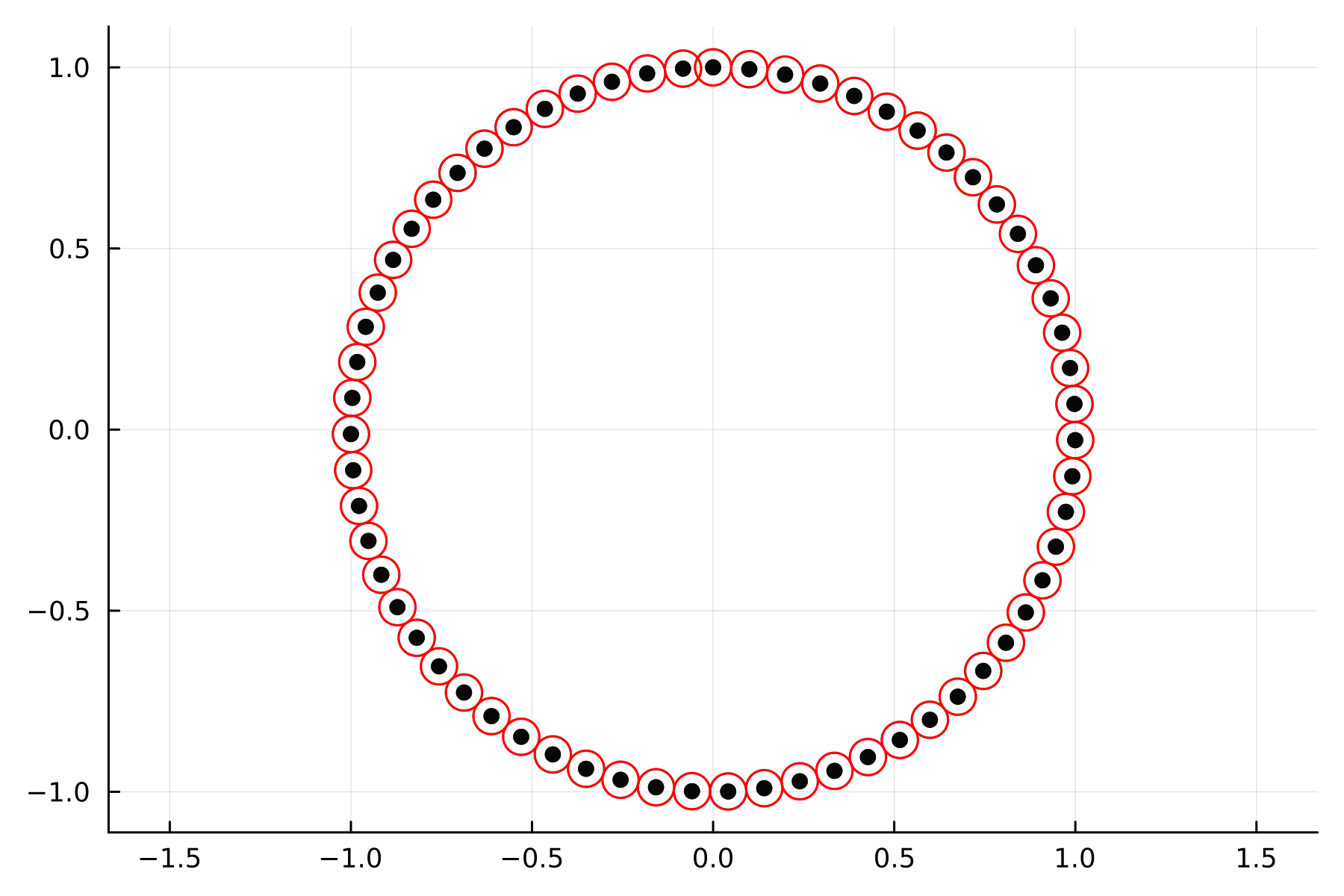

Lo que estamos viendo es justamente cómo evolucionó nuestra "cajita" de condiciones iniciales. Lo que pasa con el oscilador armónico es que es tan estable que básicamente nuestra vecindad de condición iniciales no se deformó.

Para visualizar rápidamente un sistema en el que si podamos ver deformaciones, fijémonos en el siguiente sistema artificial:

$$\begin{align*} \dot{u}_1 &= -u_1^2 + u_2 \\ \dot{u}_2 &= u_1 u_2 - 3u_2^2 \end{align*}$$

y haciendo el procedimiento anterior tendríamos:

function artificial_ode(du, u, p, t)
    du[1] = -u[1]^2 + u[2]
    du[2] = u[1]*u[2] - 3.0*u[2]^2
end

Ahora, para hacer una mejor visualización únicamente resolvamos en pocos stamps de tiempo, digamos 9 momentos tal que:

t0 = 0.0

tf = 1.7

step = 0.2

time_vector = t0:step:tf

order = 15

abstol = 1e-16

Con la siguiente condición inicial:

inic_cond = [0.1, sqrt(0.7/3)]

Resolvemos tradicionalmente:

solution1 = taylorinteg(modified_artificial_ode, inic_cond, time_vector, order, abstol, maxsteps=5000)

9×2 transpose(::Matrix{Float64}) with eltype Float64:
 0.1       0.483046
 0.181621  0.38423
 0.242864  0.324623
 0.289306  0.285386
 0.324528  0.257969
 0.351101  0.237947
 0.370964  0.222811
 0.38562   0.21104
 0.396243  0.20166

Veamos la solución

scatter(solution1[:,1], solution1[:,2], color=:black, alpha = 0.7, aspect_ratio=:equal, dpi=300)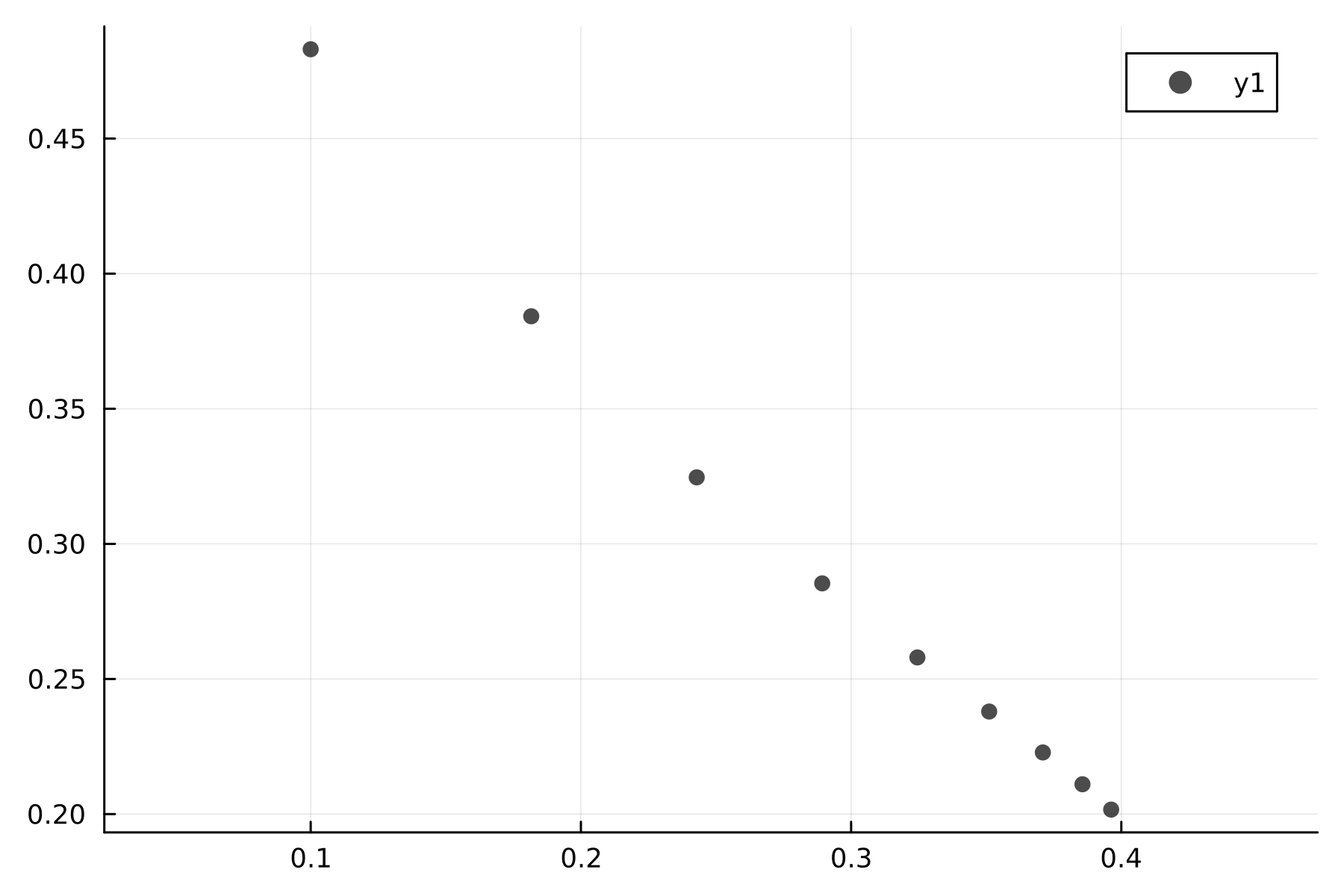

Entonces continuamos haciendo Jet Transport como ya vimos:

varorder = 16

ξ = set_variables("ξ", numvars=2, order=varorder)

q0TN = inic_cond .+ ξ

2-element Vector{TaylorN{Float64}}:
                  0.1 + 1.0 ξ₁ + 𝒪(‖x‖¹⁷)
  0.48304589153964794 + 1.0 ξ₂ + 𝒪(‖x‖¹⁷)

result = taylorinteg(modified_artificial_ode, q0TN, time_vector, order, abstol, maxsteps=5000)

Ahora volvemos a parametrizar nuestra vecindad, únicamente cambiando el tamaño del radio:

r = 0.1

ϕ = 0.0:0.1:(2π+0.1)

ξv = polar2cart.(r, ϕ)

64-element Vector{Vector{Float64}}:
 [0.1, 0.0]
 [0.09950041652780259, 0.009983341664682815]
 [0.09800665778412417, 0.019866933079506124]
 [0.09553364891256061, 0.029552020666133962]
 [0.09210609940028852, 0.03894183423086506]
 [0.08775825618903728, 0.0479425538604203]
 [0.08253356149096783, 0.05646424733950355]
 [0.07648421872844885, 0.06442176872376912]
 [0.06967067093471654, 0.07173560908995229]
 [0.06216099682706644, 0.07833269096274835]
 ⋮
 [0.070866977429126, -0.0705540325570392]
 [0.07755658785102502, -0.06312666378723208]
 [0.08347127848391599, -0.05506855425976376]
 [0.08855195169413194, -0.04646021794137566]
 [0.09274784307440359, -0.0373876664830236]
 [0.0960170286650366, -0.027941549819892587]
 [0.09832684384425848, -0.018216250427209504]
 [0.09965420970232175, -0.00830894028174964]
 [0.09998586363834151, 0.0016813900484350603]

Como ya vimos, lo que ahora esperamos al evaluar serían 9 resultados, uno para cada tiempo, donde cada resultado tiene 64 elementos, uno para cada condición inicial.

xjet_plot2 = map(λ->λ.(ξv), result[:,1])

vjet_plot2 = map(λ->λ.(ξv), result[:,2])

9-element Vector{Vector{Float64}}:
 [0.48304589153964794, 0.4930292332043308, 0.5029128246191541, 0.5125979122057819, 0.521987725770513, 0.5309884454000683, 0.5395101388791514, 0.5474676602634171, 0.5547815006296002, 0.5613785825023963  …  0.40576944278404925, 0.41249185898260876, 0.41991922775241586, 0.4279773372798842, 0.4365856735982723, 0.44565822505662434, 0.45510434171975533, 0.46482964111243846, 0.4747369512578983, 0.484727281588083]
… 
 [0.21446650874417997, 0.21599917804775967, 0.21735744115365538, 0.21853055156325896, 0.2195100837417863, 0.22028983268959196, 0.22086569951849594, 0.22123557176582911, 0.22139920508078487, 0.2213581108818932  …  0.1961314541460118, 0.19837661973931442, 0.20063818655041085, 0.2028882297349541, 0.20509960381506406, 0.20724643772399043, 0.2093045439439747, 0.21125173519024074, 0.21306804930520704, 0.21473588878687525]

Entonces, ahora visualicemos:

plot(xjet_plot2, vjet_plot2, legend=false, color=:red)

scatter!(solution1[:,1], solution1[:,2], color=:black, alpha = 0.7)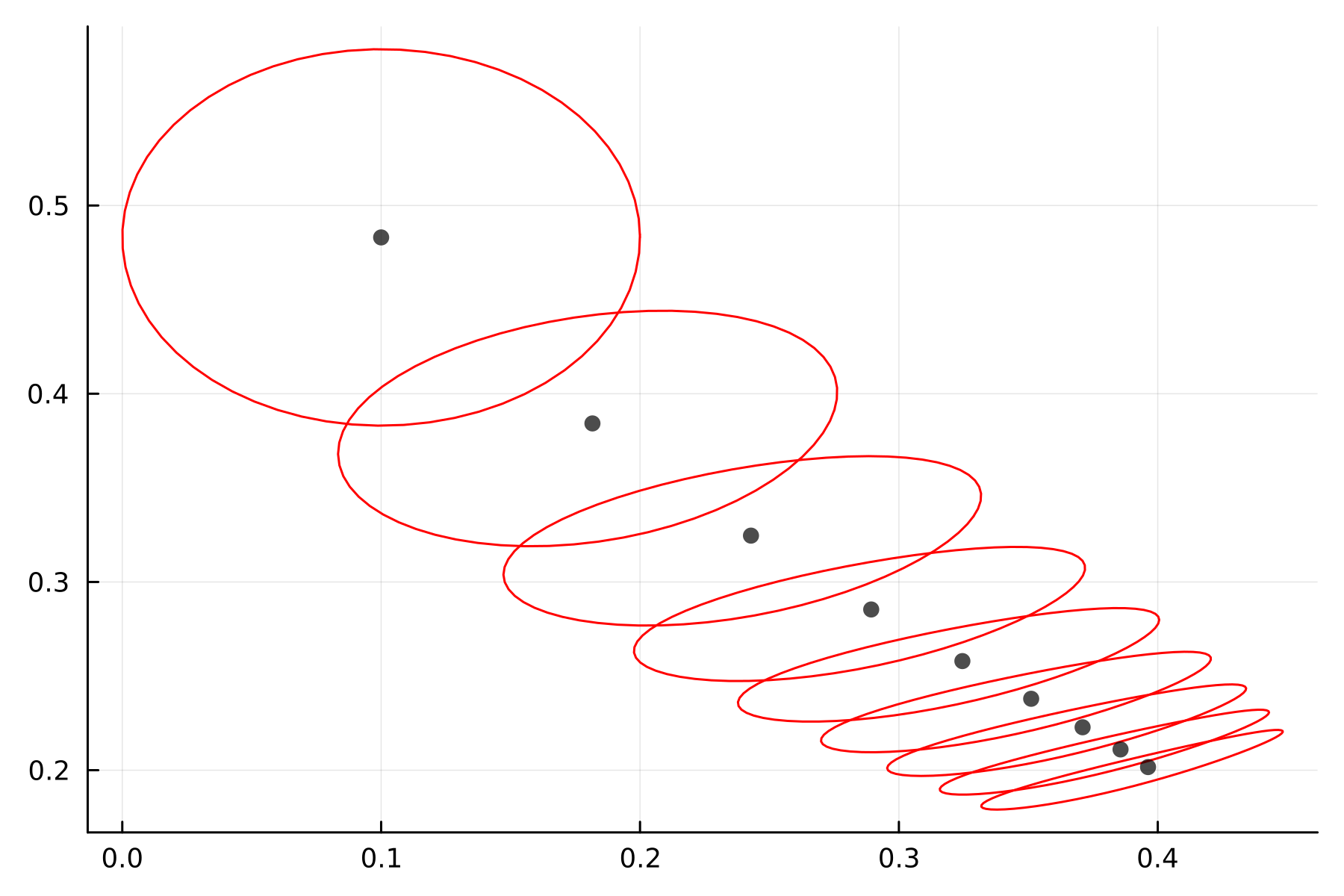

Como podemos observar, ahora sí hay claras deformaciones de nuestra "cajita". Hay demasiadas cosas interesantes que se pueden explorar y que pueden salir de este método, en este breve caso lo que lo hace particularmente valioso es que nos permite analizar el comportamiento de una vecindad completa de condiciones iniciales en un solo proceso computacional.