Análisis de estabilidad

El tratamiendo que se ha tenido hasta ahora sobre la estabilidad se ha sentido poco riguroso, pero tal vez con lo siguiente, la entrada anterior tenga un poco más de sentido formal.

Sea $x^*$ un punto fijo, entonces podemos definir una pequeña perturbación alrededor del punto como $u(t) = x(t) - x^*$. Para ver si la perturbación crece o decae nos podemos fijar en su derivada:

$$\dot{u}(t) = \frac{d}{dt}(x(t) - x^*) = \dot{x}$$

Entonces, $\dot{u} = \dot{x} = f(x)$, pero teníamos que $u(t) = x(t) - x^*$, entonces $x = x^* + u$, por lo tanto:

$$\dot{u} = \dot{x} = f(x) = f(x^* + u)$$

Por Taylor sabemos que

$$f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} (x-a)^n$$

Donde $f^{(n)}(a)$ es la $n$-ésima derivada de $f$ evaluada en $a$.

Para el caso de $f(x^* + u)$, donde $x^*$ es el punto alrededor del cual se está expandiendo y como $(x-a)^n = (x-x^*)^n = u^n$, la fórmula se convierte en:

$$f(x^* + u) = \sum_{n=0}^{\infty} \frac{f^{(n)}(x^*)}{n!} u^n$$

entonces, tendríamos que:

$$f(x^* + u) \approx f(x^*) + f'(x^*) \cdot u + \frac{1}{2} f''(x^*) \cdot u^2 + ...$$ $$f(x^* + u) = f(x^*) + f'(x^*) \cdot u + \mathcal{O}(u^2)$$

Pero recordemos que $x^*$ es un punto fijo, entonces $f(x^*) = 0$, por lo que:

$$f(x^* + u) = \dot{u}(t) = f'(x^*) \cdot u + \mathcal{O}(u^2)$$

Si $f'(x^*) \neq 0$ entonces los términos de mayor orden son pequeños y podemos ignorarlos, por lo que finalmente tendríamos que

$$\dot{u} \approx f'(x^*)\cdot u$$

Vemos que tenemos una ecuación diferencial lineal, entonces lo que acabamos de hacer es simplemente una linearización.

Ahora, si observamos bien, $f'(x^*)$ es una derivada evaluada, entonces es una constante, por lo que tenemos algo del tipo

$$\dot{u} = cu$$

este tipo de ecuaciones diferenciales las conocemos bien, en donde sabemos que $u = ke^{ct}$ si $c > 0$ y $u = ke^{-ct}$ si $c < 0$.

Esto nos dice que si $f'(x^*) > 0$ entonces $u(t)$ crece exponencialmente, y si $f'(x^*) < 0$ entonces $u(t)$ decae exponencialmente.

Si es que si $f'(x^*) = 0$ entonces no podemos ingnorar los términos de orden superior $\mathcal{O}(u^2)$ y un análisis no lineal es necesario.

La moraleja de todo esto es que la pendiente si $f'(x^*)$ en el punto fijo determina el tipo de estabilidad.

Pues podemos observar que una pendiente es negativa en los puntos fijos estables, y positiva en los inestables.

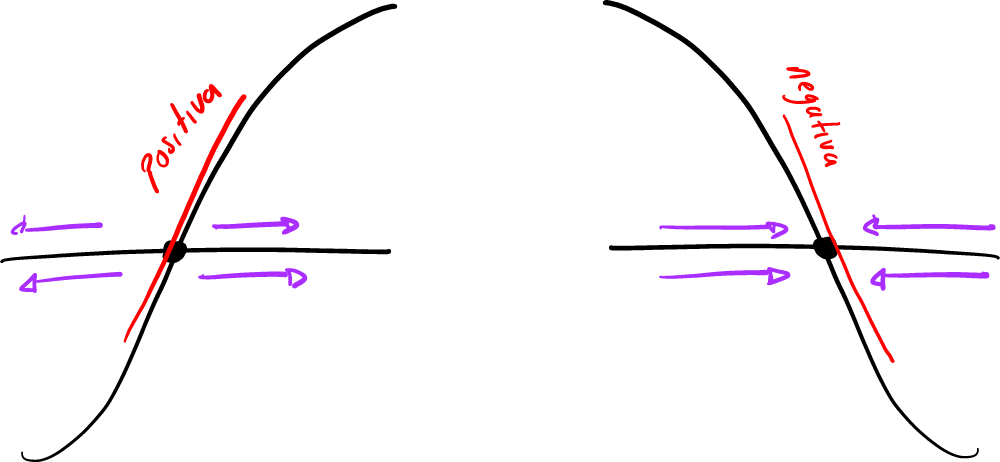
Parece que ahora tenemos simplemente una herramienta un poco más formal, mas analítica, de saber si un punto fijo es estable o inestable. Esto ya lo podíamos saber usando el análisis gráfico del que se había hablado antes, por lo que la verdadera novedad que nos trae este análisis es que ahora podemos saber qué tan estable es un punto estable, o viceversa, qué tan inestable es un punto inestable. Esto los sabemos con la magnitud de $f'(x^*)$.

También es importante porque su recíproco $\frac{1}{|f'(x^*)|}$ es lo que llamamos escala de tiempo característica, y esta es una medida de cuánto tiempo tarda un sistema en mostrar cambios significativos en su comportamiento en las cercanías del punto fijo.

Ejemplo con el caso anterior

En la entrada anterior teníamos la ecuación diferencial

$$\dot{x} = \sin{x}$$

y sabemos que los puntos fijos, es decir, cuando $\dot{x} = 0$ los tenemos cuando $\sin{x} = 0$, entonces cuando $x^* = k\pi$, por lo que

$$f'(x^*) = \cos k\pi = \begin{cases} 1, & k \text{ par} \\ -1, & k \text{ impar} \end{cases}$$

por lo tanto, si $k$ es par, tenemos punto inestable, si $k$ es impart, tenemos punto estable. Confirmando lo que obtuvimos en el análisis gráfico.

---

Ejemplo con la ecuación logística

La ecuación logística es una ecuación diferencial que modela el crecimiento de una población limitada por factores ambientales y recursos, su forma más común es:

$$\dot{P} = f(P) = rP \left(1 - \frac{P}{K}\right)$$

donde:

• $P$ es la población en el tiempo $t$,

• $r$ es la tasa de crecimiento intrínseca,

• $K$ es la capacidad de carga del ambiente, es decir, el tamaño máximo de la población que el ambiente puede soportar.

Para encontrar los puntos fijos, tenemos que resolver tal que:

$$rP \left(1 - \frac{P}{K}\right) = 0$$

Para que esta ecuación sea cero, uno de los factores en el producto debe ser cero:

1. $rP = 0$

2. $1 - \frac{P}{K} = 0$

Dado que $r$ es la tasa de crecimiento intrínseca y no puede ser cero (pues implicaría que no hay crecimiento), entonces, los puntos fijos son:

$$P = 0$$ $$P = K$$

Derivando tenemos que

$$f'(P) = r \left(1 - \frac{2P}{K}\right)$$

Ahora sustituimos los puntos fijos $P = 0$ y $P = K$ en esta derivada para determinar la estabilidad de cada punto fijo.

Para $P = 0$:

$$r \left(1 - \frac{2(0)}{K}\right) = r \left(1 - 0\right) = r$$

Para $P = K$:

$$r \left(1 - \frac{2K}{K}\right) = r \left(1 - 2\right) = r (-1) = -r$$

En resumen:

• $P = 0$ es un punto fijo inestable.

• $P = K$ es un punto fijo estable.

Podemos calcular la escala de tiempo característica, pues sabemos que $\tau = \frac{1}{|f'(x^*)|}$, tendríamos que:

$$\tau = \frac{1}{|f'(x^*)|} = \frac{1}{r}$$

Esto significa que cuanto mayor sea la tasa de crecimiento $r$, más rápido la población se acercará a su capacidad de carga $K$.