Ecuaciones diferenciales como campos vectoriales

Supongamos que queremos resolver la siguiente ecuación diferencial:

$$\dot{x} = \sin{x}$$

Esto podríamos hacerlo analíticamente, de la siguiente forma:

$$\begin{aligned} \dot{x} &= \sin{x} \\ \frac{dx}{dt} &= \sin{x} \\ \frac{dx}{\sin{x}} &= dt \\ \int \frac{dx}{\sin{x}} &= \int dt \\ \end{aligned}$$ $$-\ln|\csc{x} + \cot{x}| + C = t$$

Si suponemos que $x = x_0$ en $t = 0$ , entonces:

$$-\ln|\csc{x_0} + \cot{x_0}| + C = 0$$ $$C = \ln|\csc{x_0} + \cot{x_0}| \\$$

Por lo tanto, nuestra solución nos quedaría:

$$t = \ln{|\frac{\csc{x_0} + \cot{x_0}}{\csc{x} + \cot{x}}|}$$

Nuestra solución está medio aburrida, la verdad es que no nos dice mucho.

¿Qué haríamos si nos interesara saber qué es lo que pasa con nuestra solución cuando la condición inicial es $x_0 = \pi / 4$ para $t > 0$ ?

Podemos hacer un análisis, gráfico de la siguiente forma:

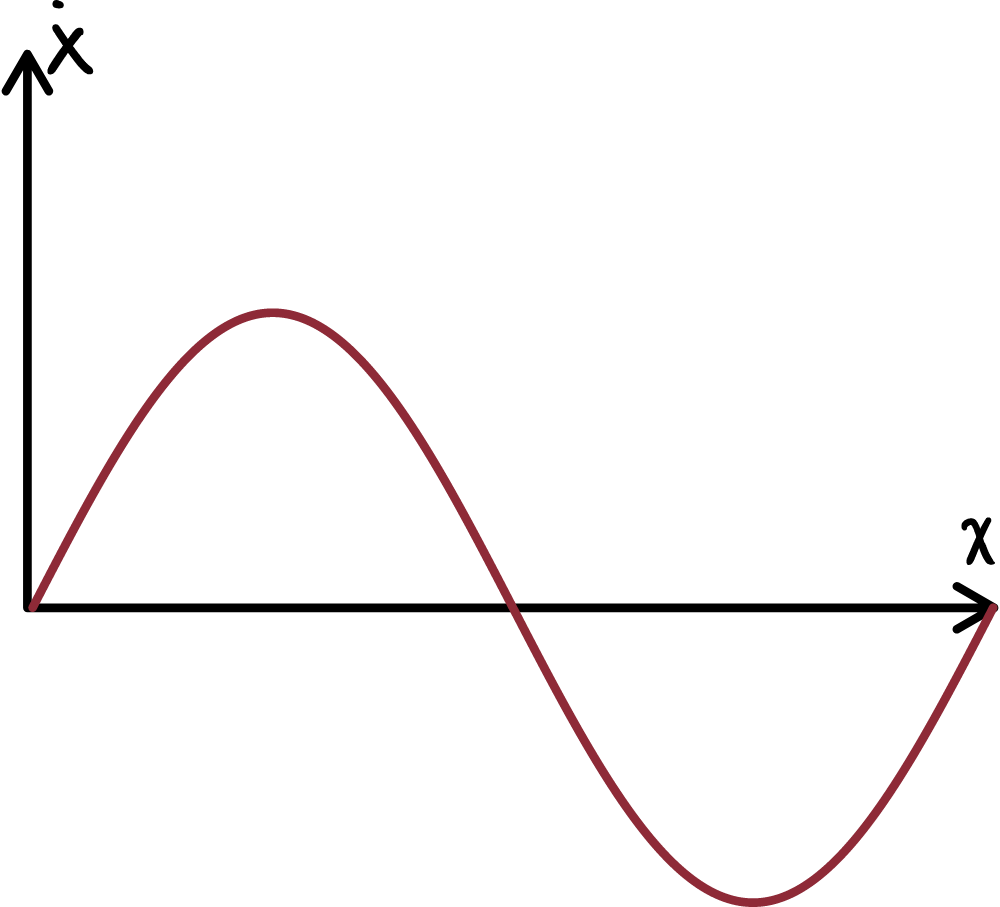
Tenemos que $\dot{x} = \sin{x} = f(x)$ graficando, nos encontraríamos únicamente con un seno

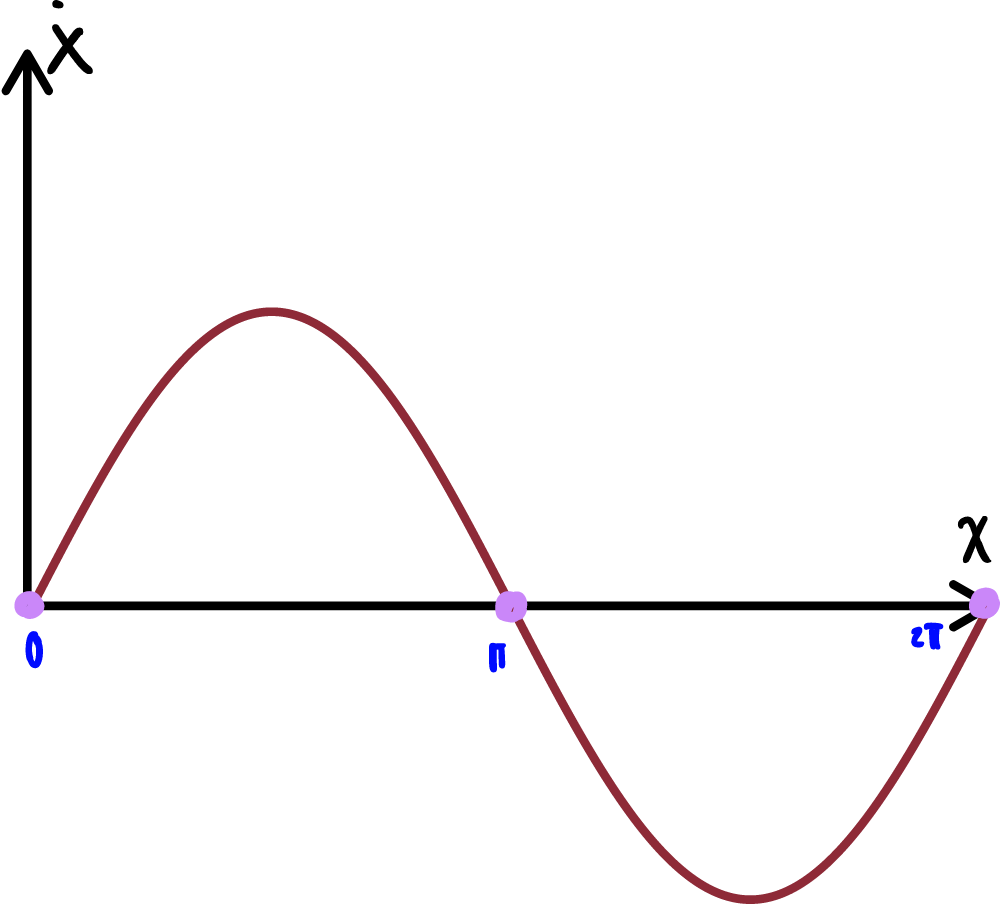
Ahora, ubicamos los puntos fijos, como sabemos estos son donde $\dot{x} = \sin{x} = 0$

Podemos pensar en que, cuando la velocidad, es decir, el eje $y$ de nuestra gráfica, es positiva, entonces una especie de flujo imaginario, fluye hacia la derecha, controlando la dirección de la dinámica en esos puntos. Y de la misma forma, si la velocidad es negativa, entonces se fluye hacia la izquierda.

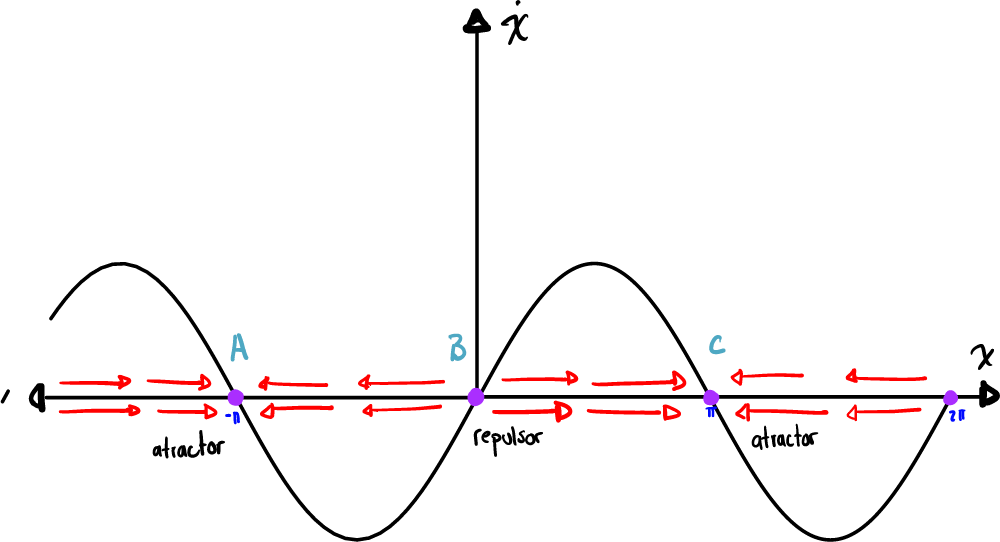
Tenemos tres puntos; A, B y C. Si observamos cómo nos quedaron las direcciones del flujo alrededor de nuestros puntos fijos, tomando en cuenta la dirección de la velocidad, notamos que A es un punto atractor, pues de alguna forma parece ser que el flujo es atraído a este punto, B es un repulsor, el flujo parece huir de este punto, y finalmente, C también es atractor.

Ahora pensemos, supongamos que nos paramos en un punto atractor, ahí estamos a salvo, pues es un punto en donde no hay dinámica, en donde $\dot{x} = 0$, ¿pero qué pasa si nos movemos un poquito? Como nos encontramos en un punto atractor, parece que a donde sea que nos movamos, vamos en dirección contraria al flujo, entonces la dinámica del sistema no me está dejando que me vaya del punto fijo en el que me encuentro, entonces estamos parados en un punto fijo estable.

Si nos paramos en un repulsor, y nos movemos tantito, ahora para donde sea que vayamos, iríamos con la dirección del flujo, por lo que movernos tantito, significaría abandonar el punto fijo. Entonces estaríamos parados en un punto fijo inestable.

Por lo tanto, eso es lo que pasa, un atractor es un punto fijo estable, un repulsor es un punto fijo inestable.

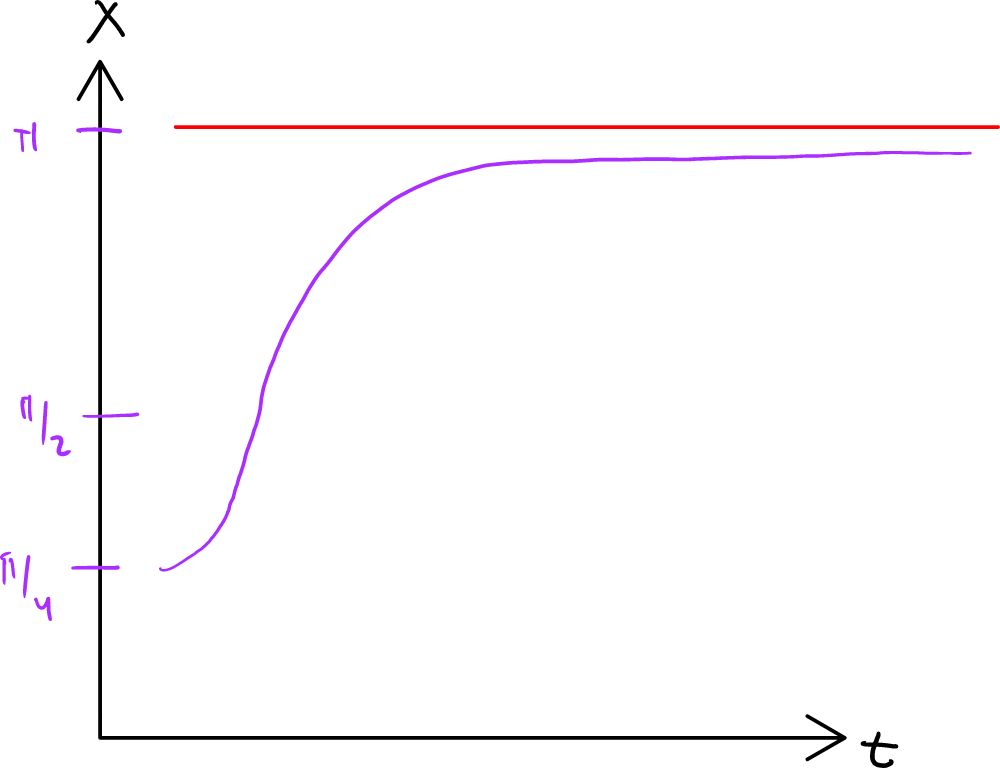
Hace un rato nos preguntamos: ¿Qué haríamos si nos interesara saber qué es lo que pasa con nuestra solución cuando la condición inicial es $x_0 = \pi / 4$ para $t > 0$ ?

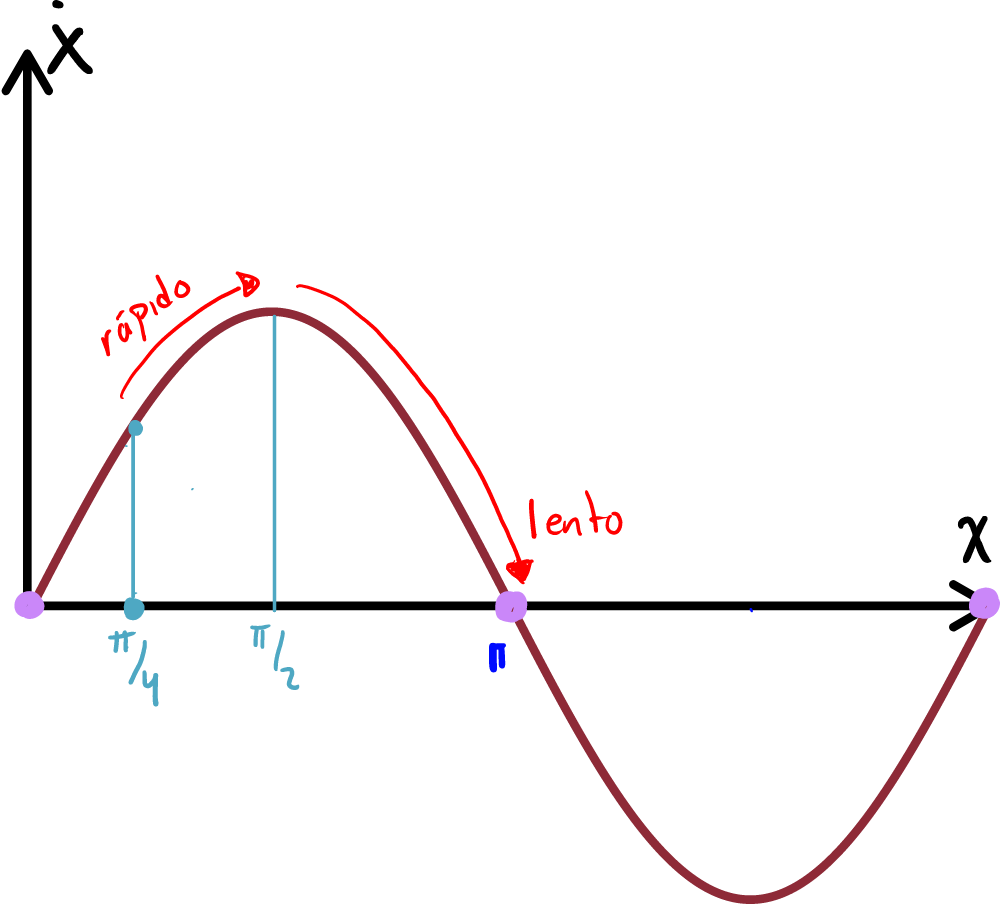
Si hacemos un análisis gráfico, podemos ver que si partimos de $\pi / 4$ el flujo nos llevaría de forma rápida hasta $\pi / 2$, llegando a este punto, seguiríamos moviéndonos en la misma dirección, pues la velocidad sigue siendo positiva, pero iríamos cada vez más lento, dirigiéndonos a $\pi$ de forma asintótica.