Existencia y unicidad

Antes de hablar de existencia y unicidad vale la pena repasar un concepto clave.

Regresando al péndulo simple, teníamos que el sistema está descrito por:

entonces, tener una solución sería tener un par de funciones, \(x_1(t)\) y \(x_2(t)\), una para la posición y otra para la velocidad del péndulo.

Con esto, podemos construir un espacio abstracto con coordenadas \( (x_1, x_2) \), aquí nuestra solución \((x_1(t) , x_2(t))\) correspondería a un punto moviéndose a través de una curva en este espacio.

Esta curva es lo que llamamos trayectoria, y el espacio abstracto es lo que llamamos espacio-fase. Este espacio-fase está lleno de trayectorias, pues cada punto puede servir como una condición inicial.

Veamos, juguemos un poquito con código para visualizar esto:

Primero cargamos las paqueterías que necesitamos:

using DifferentialEquations, Plots

Ahora definimos el sistema en una función, le damos unos valores simples a los parámetros, elegimos algunas condiciones iniciales y un span de tiempo para hacer la integración.

# Definir la ecuación diferencial
function pendulum(dx, x, p, t)
    dx[1] = x[2]
    dx[2] = -(g/L) * sin(x[1])
end

x0 = [0.5, 0.5] # Condición inicial
g, L = 1.0, 1.0 # Parámetros
tspan = (0.0, 15.0) # Intervalo de tiempo

Ahora definimos el problema como ya se ha visto aquí.

# Definimos el problema
prob = ODEProblem(pendulum, x0, tspan)

# Resolver el problema
sol = solve(prob)

# Graficamos la solución, el índice 1 (posición) vs índice 2 (velocidad)
plot(sol, 
    idxs=(1,2), 
    xlabel="x", 
    ylabel="v",
    title="Diagrama de Fase",
    label="Trayectoria",
    aspect_ratio=:equal,
    grid=false
)

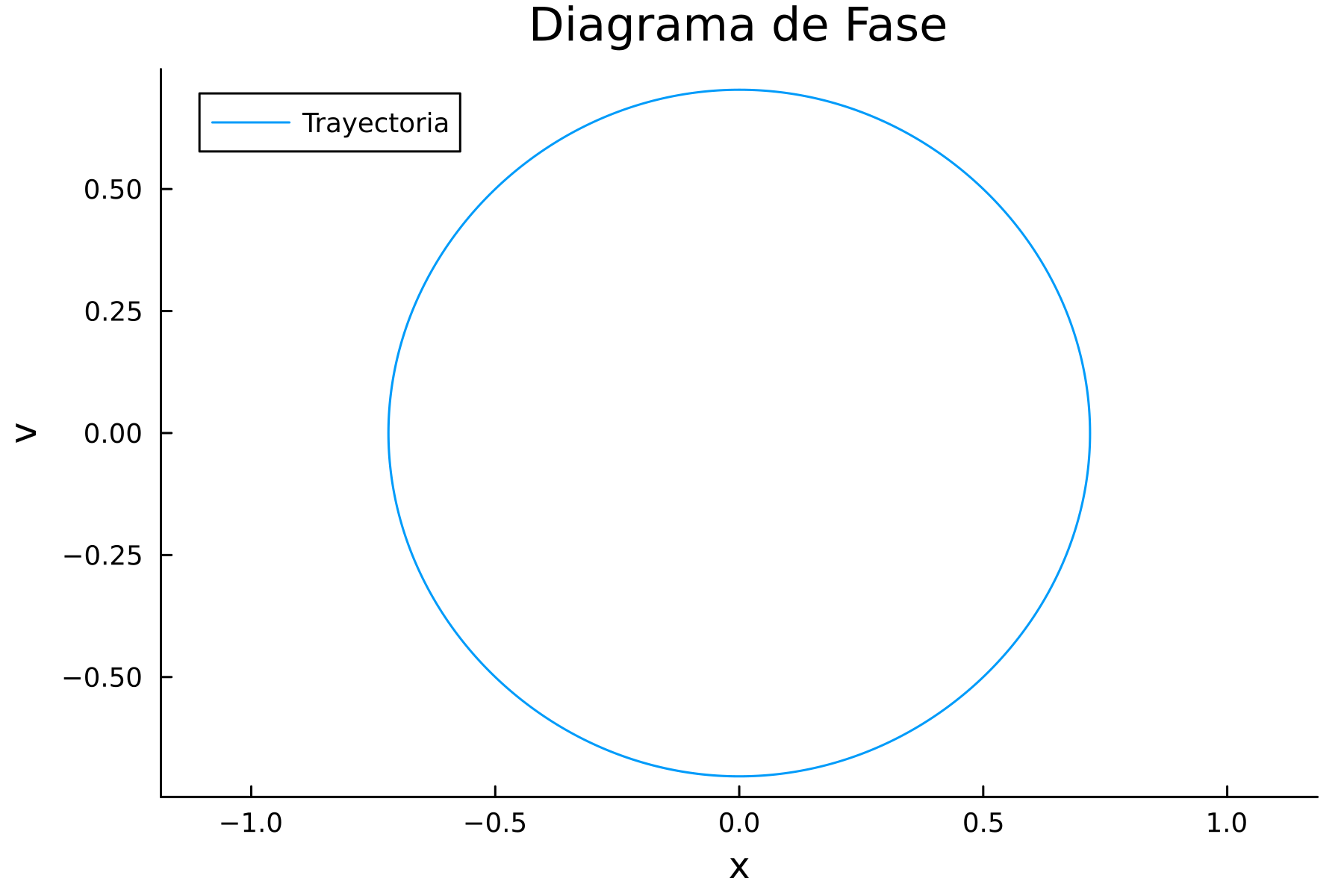
Podemos observar la trayectoria para el péndulo simple con posición inicial \(0.5\) y velocidad inicial \(0.5\).

Tal vez ahora, para visualizar mejor el concepto de espacio-fase, sea útil observar más trayectorias.

Definamos unas nuevas condiciones iniciales:

initial_conditions = [
    [0.0, 0.0],    # Equilibrio estable
    [π, 0.0],      # Equilibrio inestable
    [π/2, 0.0],    # Posición horizontal, sin velocidad inicial
    [-π/2, 0.0],   # Posición horizontal opuesta, sin velocidad inicial
    [π/4, 1.0],    # 45 grados con velocidad positiva
    [-π/4, -1.0],  # -45 grados con velocidad negativa
    [0.0, 2.0],    # Posición vertical con alta velocidad inicial
    [0.0, -2.0],   # Posición vertical con alta velocidad inicial negativa
    [π/3, 0.5],    # 60 grados con velocidad moderada
    [-π/3, -0.5],  # -60 grados con velocidad moderada negativa
    [2π/3, 0.0],   # 120 grados sin velocidad inicial
    [-2π/3, 0.0],  # -120 grados sin velocidad inicial
    [π/6, 1.5],    # 30 grados con alta velocidad
    [-π/6, -1.5],  # -30 grados con alta velocidad negativa
    [5π/6, 0.2]    # 150 grados con baja velocidad
]

Y entonces resolvemos de la misma forma para cada una de las condiciones iniciales y graficamos en un solo plot cada una de las trayectorias resultantes;

# Crear un plot vacío
plot()

# Resolver y graficar para cada condición inicial
for x0 in initial_conditions
    prob = ODEProblem(pendulum, x0, tspan)
    sol = solve(prob)
    
    # Graficar el espacio de fase
    plot!(sol, idxs=(1,2), linewidth=2)
end

# Mostrar el plot
plot!( 
    xlabel="x", 
    ylabel="v",
    title="Espacio-Fase",
    legend=false,
    aspect_ratio=:equal,
    grid=false
)

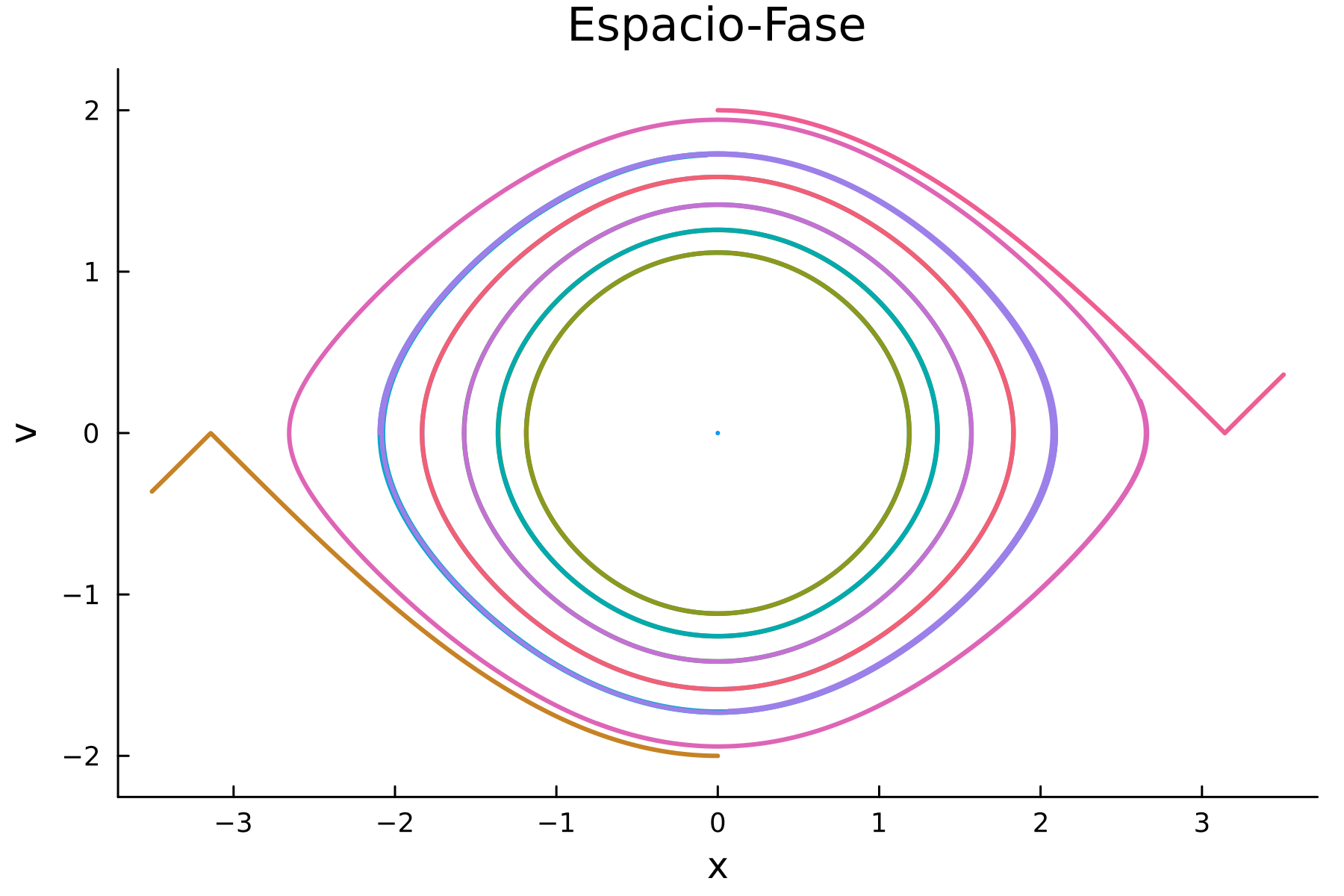
Lo que estamos viendo es cómo se va llenando el espacio fase de trayectorias.

Si googleamos el espacio de fase de un péndulo, podemos ver resultados parecidos a lo que acabamos de obtener:

---

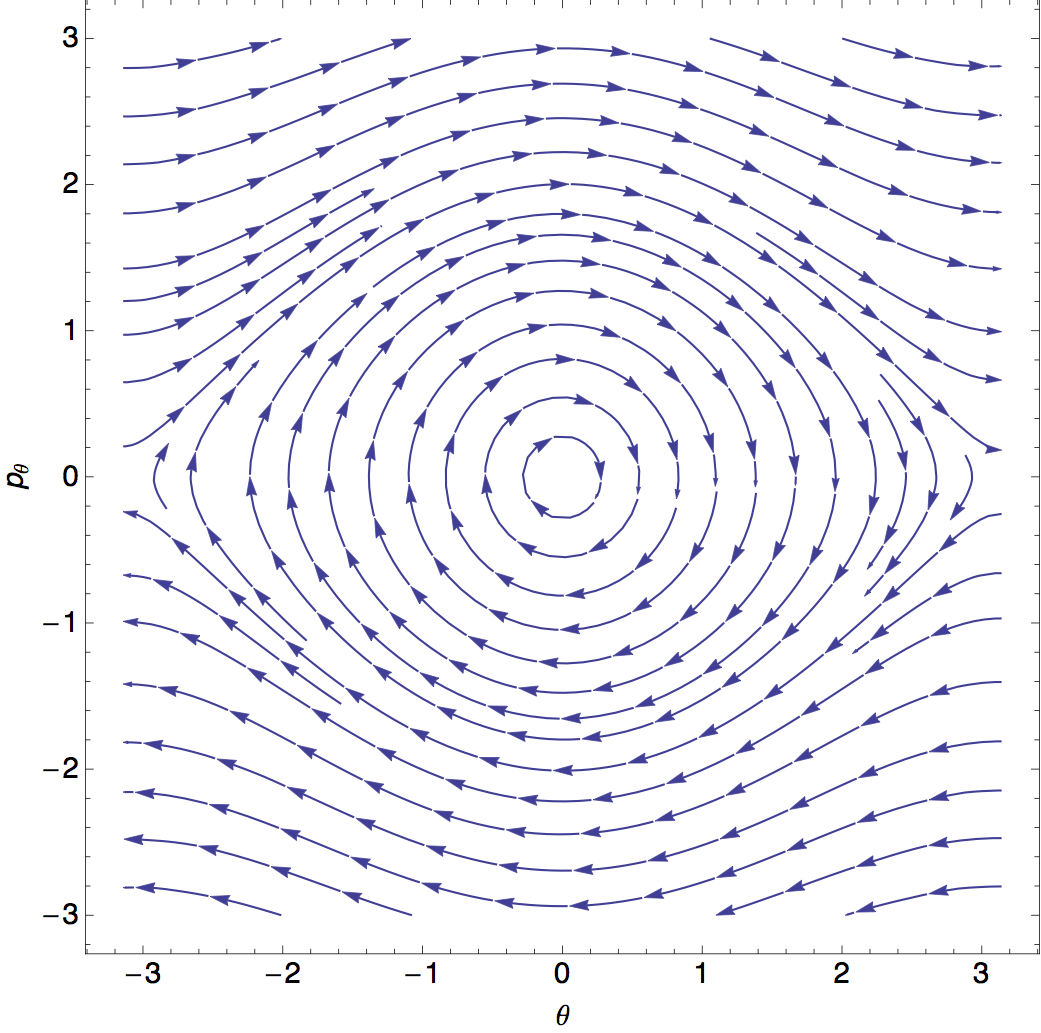
Ahora sí, regresando al punto de esta entrada. Hay que ser honestos, hasta ahora, el tratamiendo que se le ha dado a todos nuestros análisis se siente informal.

En primer lugar, se discutió las soluciones de las ecuaciones del tipo: \( \dot{x} = f(x) \), pero, para empezar, ¿qué nos garantiza que la solución que buscamos exista?, y más aún, que sea única.

Pensemos en un caso que parece simple, la ecuación:

\[ \dot{x} = x^{1/3} \quad\quad \text{con}\quad\quad x(0) = 0 \]

una solución claramente es la solución trivial, \( x = 0 \). Pero...

Resolvamos analíticamente:

\[ \frac{dx}{dt} = x^{1/3} \] \[ x^{-1/3} \, dx = dt \] \[ \int x^{-1/3} \, dx = \int dt \] \[ \frac{3}{2} x^{2/3} + C_1 = t + C_2 \] \[ \frac{3}{2} x^{2/3} = t + C \]

Usamos la condición inicial \(x(0) = 0\) para encontrar \(C\). Cuando \(t = 0\), \(x = 0\), por lo tanto:

\[ \frac{3}{2} (0)^{2/3} = 0 + C \implies C = 0 \]

Así que la ecuación simplificada es:

\[ \frac{3}{2} x^{2/3} = t \]

Despejamos \(x\) para obtener la solución explícita:

\[ x^{2/3} = \frac{2}{3} t \] \[ x = \left( \frac{2}{3} t \right)^{3/2} \]

Y esta última también es solución. Entonces, ¿cuál es la buena?

Pues es complicado, aquí cualquier análisis que hemos visto fallaría, porque a ver, la solución \(x(t) = 0\) nos dice que para la condición inicial dada, la partícula ni siquiera se movería. Pero la otra solución, que obtuvimos nos dice que seguiría una trayectoria, entonces, el punto-fase en el origen en nuestro espacio-fase no sabría qué hacer. De hecho, todo se pone peor, porque se puede demostrar que las soluciones son infinitas.

Todo esto se empieza a esclarecer si le echamos un ojo al teorema de Picard–Lindelöf, o también conocido como teorema de existencia y unicidad, este nos dice que:

Sea \(D \subseteq \mathbb{R} \times \mathbb{R}^n\) un rectángulo cerrado con \((t_0, y_0) \in \text{int}(D)\), el interior de \(D\). Sea \(f: D \rightarrow \mathbb{R}^n\) una función que es continua en \(t\) y Lipschitz continua en \(y\) (con constante de Lipschitz independiente de \(t\)). Entonces, existe algún \(\varepsilon > 0\) tal que el problema de valor inicial \(y'(t) = f(t, y(t)), \quad y(t_0) = y_0\) tiene una solución única \(y(t)\) en el intervalo \([t_0 - \varepsilon, t_0 + \varepsilon]\).

En español, nos dice que todo jala bien siempre y cuando nuestra función sea continua en t y Lipschitz continua en y. Básicamente que sea Lipschitz significa que existe una constante \(L\) tal que la tasa de cambio entre dos puntos no supere esta constante. Esto es una forma de decirnos que es continua, peroq ue no cambia tan rápido en tal punto.

Para que no nos vayamos tan lejos, observemos la función:

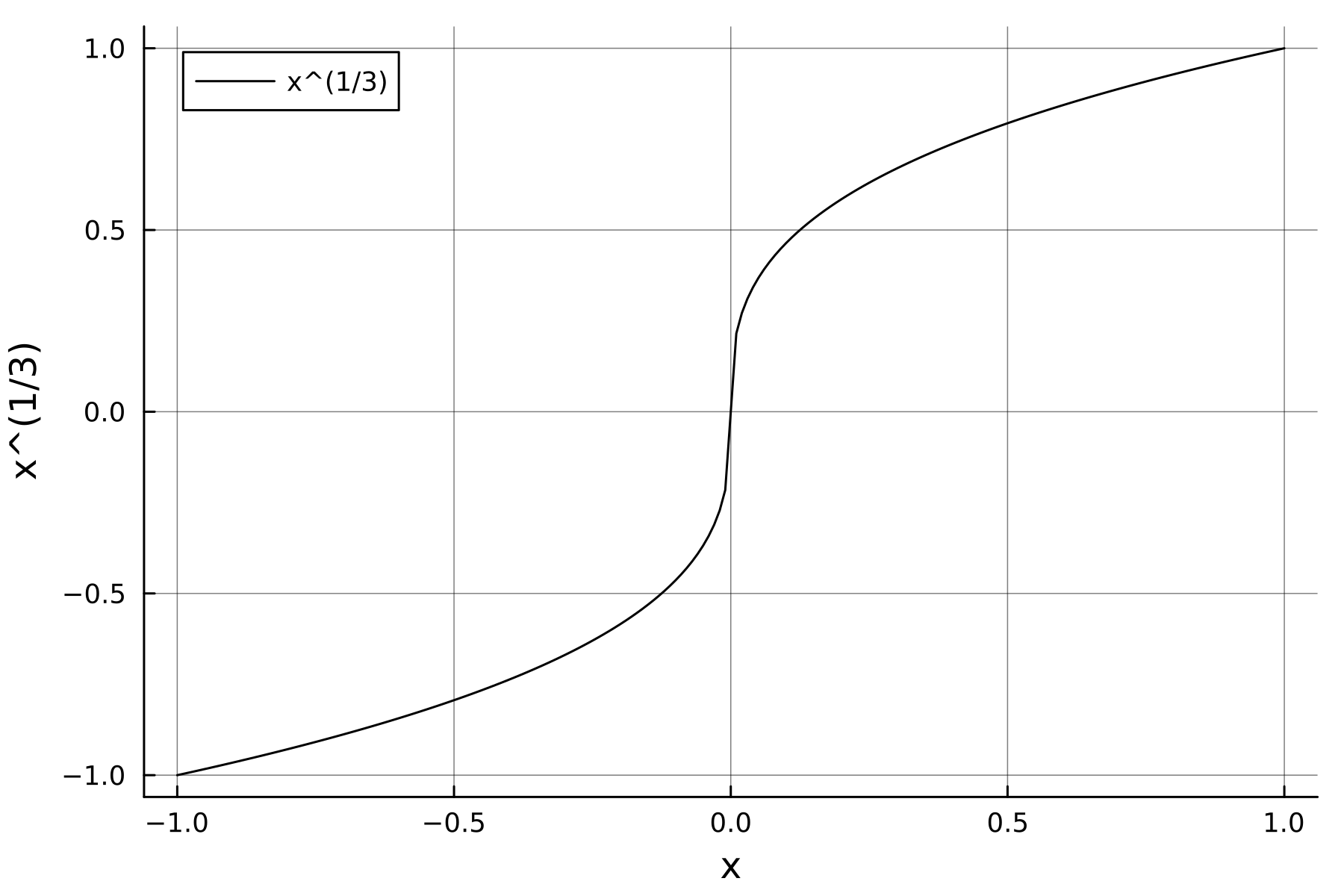
Es claro que en 0 no es Lipschitz continua, pues de hecho \(f'(0)\) es infinito.

Por lo tanto, este teorema nos dice que si \(f(x)\) está lo suficientemente bonita, la solución existe y es única.