Algo importante que debemos hacer ahora es encontrar las derivadas o tasas de cambio de los vectores base $\{ \mathbf{e}'_1, \mathbf{e}'_2, \mathbf{e}'_3 \}$, esos que se están moviendo con el marco de referencia $\mathcal{F}´$. Estos vectores son constantes en el marco de referencia inercial, pero desde el marco de referencia "real", no lo son, claramente se están moviendo, por lo que nos interesa obtener es la derivada "real".

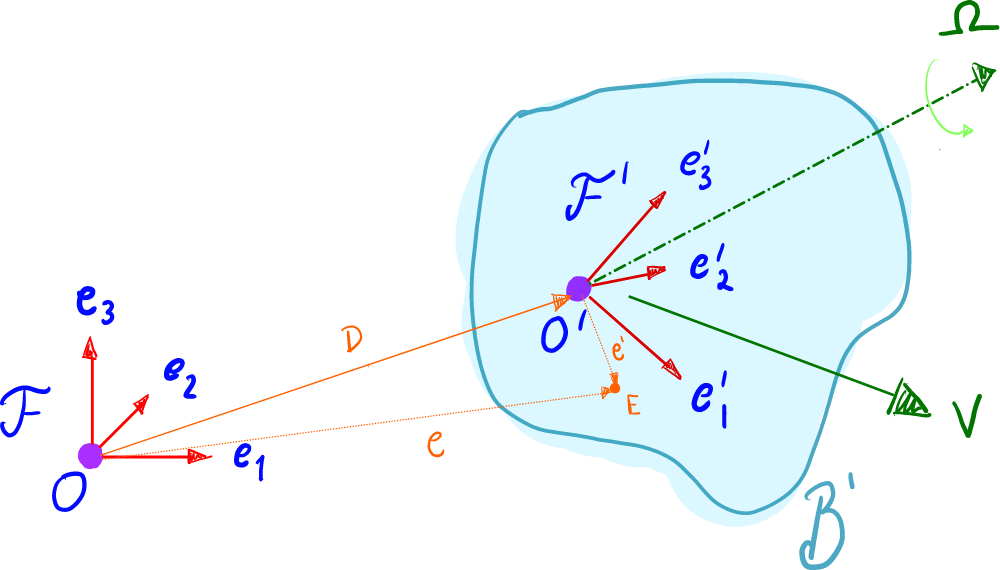
Pensemos en una partícula $E$ que pertenece al cuerpo $\mathcal{B'}$ en el cual el marco $\mathcal{F'}$ está embuido, entonces sea $\mathbf{e}$ y $\mathbf{e'}$ vectores posición de $E$ relativos a $O$ y $O'$ respectivamente.

Entonces,

$$\mathbf{e} = \mathbf{D} + \mathbf{e'}$$

donde como vemos, $\mathbf{D}$ es el vector posición de $O'$ relativo a $O$.

por lo que:

$$\left( \frac{d\mathbf{e}}{dt} \right) _{\mathcal{F}} = \left(\frac{d \mathbf{D}}{dt}\right)_{\mathcal{F}} + \left(\frac{d \mathbf{e'}}{dt}\right)_{\mathcal{F}}$$ $$= \mathbf{V} + \left(\frac{d \mathbf{e'}}{dt}\right)_{\mathcal{F}}$$

en donde sabemos que $\mathbf{V}$ es la velocidad a la que se mueve $O'$ relativa a $O$. Además $\left( \frac{d\mathbf{e}}{dt} \right)_{\mathcal{F}}$ es la velocidad de la partícula $E$, entonces:

$$\mathbf{V^{E}} = \mathbf{V}^{o'} + \left( \frac{d\mathbf{e'}}{dt} \right)_{\mathcal{F}}$$

Vale la pena recordar un teorema muy importante.

Teorema: Existencia de la velocidad angular. Supongamos que un cuerpo rígido está en movimiento completamente general y sea B cualquiera de sus partículas. Entonces existe un único vector 𝜔(t) tal que la velocidad de cualquier partícula P del cuerpo está dada por la fórmula: 𝒗ᴾ = 𝒗ᴮ + 𝜔 × (𝒓 − 𝒃), donde 𝒓 y 𝒃 son los vectores posición de P y B, y 𝒗ᴮ es la velocidad de B.

Lo que nos dice este teorema es que podemos entender el movimiento de cualquier rígido como una traslación con velocidad $\mathbf{v}^{B}$ y una rotación con alguna velocidad angular $\omega$ alrededor de un eje a través de $B$.

Por lo tanto, regresando a nuestro problema, tendríamos que:

$$\begin{align*} \mathbf{V^{E}} &= \mathbf{V}^{o'} + \left( \frac{d\mathbf{e'}}{dt} \right)_{\mathcal{F}} \\ &= \mathbf{V}^{o'} + \Omega \times (\mathbf{e} - \mathbf{D}) \\ &= \mathbf{V}^{o'} + \Omega \times \mathbf{e'} \end{align*}$$

Entonces podemos concluir que

$$\left( \frac{d\mathbf{e'}}{dt} \right)_{\mathcal{F}} = \Omega\times \mathbf{e'}$$

y esto aplica para cualquier vector posición $\mathbf{e'}$ relativo a $O'$ del cuerpo $\mathcal{B'}$ y en general, como nuestra base es $(\mathbf{e_{1}', \mathbf{e_{2}}', \mathbf{e_{3}'}} )$ obtendríamos que:

$$\left( \frac{d\mathbf{e_{j}'}}{dt} \right)_{\mathcal{F}} = \Omega\times \mathbf{e_{j}'}$$ $$\therefore \quad\quad \mathbf{\dot{e}_{1}'} = \Omega\times \mathbf{e_{1}'}, \quad \mathbf{\dot{e}_{2}'} = \Omega\times \mathbf{e_{2}'}, \quad \mathbf{\dot{e}_{3}'} = \Omega\times \mathbf{e_{3}'}$$

Donde sabemos que $\Omega$ es la velocidad angular del marco $\mathcal{F}'$ relativo al marco $\mathcal{F}$.

Entonces ahora sí, lo que nos interesaba saber era cómo se veían las tasas de cambio o derivadas de cualquier cantidad vectorial $u(t)$. Primero recordamos que $\mathbf{u}$ en términos del conjunto base $\{\mathbf{e_{1}}, \mathbf{e_{2}}, \mathbf{e_{3}} \}$ es;

$$\mathbf{u} = u_{1}'\mathbf{e_{1}'} + u_{2}'\mathbf{e_{2}'} + u_{3}'\mathbf{e_{3}'}$$

Entonces:

$$\begin{align*} \left(\frac{d\mathbf{u}}{dt}\right)_{\mathcal{F}} &= \left(\frac{d(u'_{1} e'_1)}{dt}\right)_{\mathcal{F}} + \left(\frac{d(u'_{2} e'_2)}{dt}\right)_{\mathcal{F}} + \left(\frac{d(u'_{3} e'_3)}{dt}\right)_{\mathcal{F}} \\ &= (\dot{u}'_{1} e'_1 + \dot{u}'_{2} e'_2 + \dot{u}'_{3} e'_3) + u'_{1} \dot{e}'_1 + u'_{2} \dot{e}'_2 + u'_{3} \dot{e}'_3 \\ &= \left(\frac{du}{dt}\right)_{\mathcal{F'}} + u'_{1} (\Omega \times \mathbf{e}'_1) + u'_{2} (\Omega \times \mathbf{e}'_2) + u'_{3} (\Omega \times \mathbf{e}'_3) \\ &= \left(\frac{du}{dt}\right)_{\mathcal{F'}} + \Omega \times (u'_{1} \mathbf{e}'_1 + u'_{2} \mathbf{e}'_2 + u'_{3} \mathbf{e}'_3) \\ &= \left(\frac{du}{dt}\right)_{\mathcal{F'}} + \Omega \times \mathbf{u}. \end{align*}$$

Por lo tanto tendríamos que:

$$\left( \frac{d\mathbf{u}}{dt} \right)_{\mathcal{F}} = \left( \frac{d\mathbf{u}}{dt} \right)_{\mathcal{F}'} + \Omega\times \mathbf{u}$$

Ahora podemos ver cómo se transforma, por ejemplo, la velocidad entre marcos de referencia.

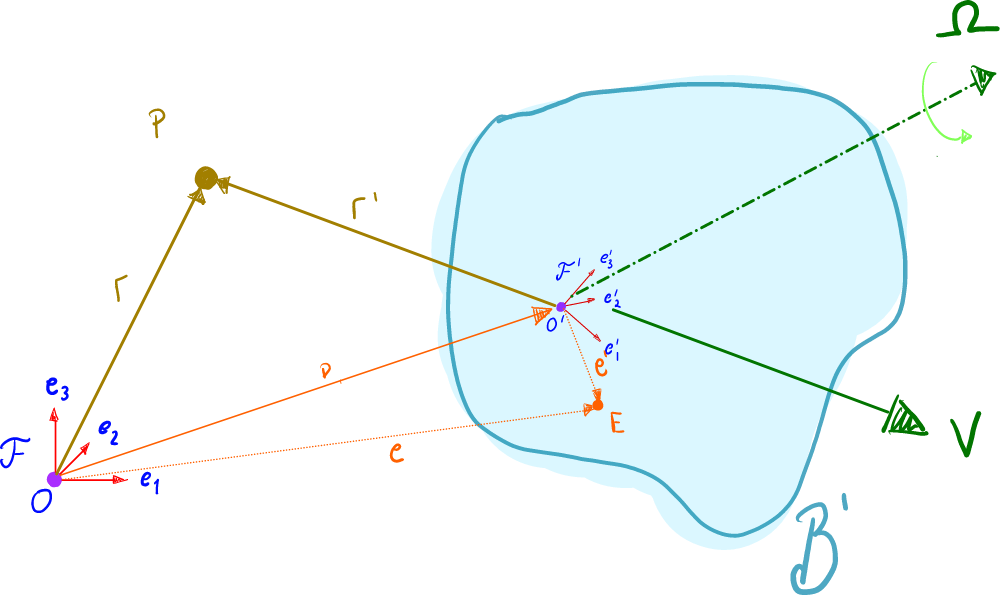
Entonces, supongamos una partícula $P$ que tiene un vector posición $\mathbf{r}$ relativo a $\mathcal{F}$ y vector posición $\mathbf{r'}$ relativo a $\mathcal{F'}$. Entonces de la misma forma tenemos que

$$\mathbf{r} = \mathbf{D} + \mathbf{r'}$$

Por lo tanto:

$$\begin{align*} \left( \frac{d\mathbf{r}}{dt} \right)_{\mathcal{F}} &= \left( \frac{d\mathbf{D}}{dt} \right)_{\mathcal{F}} + \left( \frac{d\mathbf{r'}}{dt} \right)_{\mathcal{F}} \\ \mathbf{ v}&= \mathbf{V} + \left( \frac{d\mathbf{r'}}{dt} \right)_{\mathcal{F}} \end{align*}$$

Pero ya sabemos que $\left( \frac{d\mathbf{u}}{dt} \right)_{\mathcal{F}} = \left( \frac{d\mathbf{u}}{dt} \right)_{\mathcal{F}'} + \Omega\times \mathbf{u}$, entonces tenemos que:

$$\begin{align*} \left( \frac{d\mathbf{r'}}{dt} \right)_{\mathcal{F}} &= \left( \frac{d\mathbf{r'}}{dt} \right)_{\mathcal{F}'} + \Omega\times \mathbf{r'} \\ &= \mathbf{v'} + \Omega\times \mathbf{r'} \end{align*}$$

Entonces tendríamos que:

$$\mathbf{v} = \mathbf{V} + \mathbf{v'} + \Omega\times \mathbf{r'}$$

Lo que podemos ver de esta fórmula es que, la velocidad "real" del punto $P$ es la suma de la velocidad aparente $\mathbf{v'}$ y los términos $\mathbf{V} + \Omega\times \mathbf{r'}$ que son dados por el marco de referencia no inercial. Ahora, básicamente, podemos determinar cómo se ve la velocidad de un objeto desde diferentes perspectivas, particularmente cuando uno de los sistemas de referencia se está moviendo o rotando con respecto al otro.

Para poner un ejemplo de cómo yo entiendo esa fórmula es suponiendo que nosotros, desde el suelo queremos calcular la velocidad a la que se mueve un pasajero en un avión, primero tendríamos que tomar en cuenta la velocidad a la que se mueve el avión de nosotros $\mathbf{V}$, la velocidad a la que se mueve el pasajero respecto a su marco de referencia no inercial (el avión) $\mathbf{v'}$ y finalmente, suponiendo que el avión va en una curva, es decir, rotando, entonces necesitamos el último término $\Omega\times \mathbf{r'}$.

Ahora, sabemos que para obtener la aceleración, volvemos a derivar, entonces:

$$\left( \frac{d\mathbf{v}}{dt} \right)_{\mathcal{F}} = \left( \frac{d\mathbf{V}}{dt} \right)_{\mathcal{F}}+ \left( \frac{d\mathbf{v'}}{dt} \right)_{\mathcal{F}} + \left( \frac{d}{dt} (\Omega \times \mathbf{r'}) \right)_{\mathcal{F}}$$

en donde sabemos que:

$$\frac{d}{dt} (\Omega \times \mathbf{r'}) = \frac{d\Omega}{dt} \times \mathbf{r'} + \Omega \times \frac{d\mathbf{r'}}{dt}$$

reemplazando tenemos que

$$\left( \frac{d\mathbf{v}}{dt} \right)_{\mathcal{F}} = \left( \frac{d\mathbf{V}}{dt} \right)_{\mathcal{F}}+ \left( \frac{d\mathbf{v'}}{dt} \right)_{\mathcal{F}} + \left( \frac{d\Omega}{dt} \right)_{\mathcal{F}} \times \mathbf{r'} + \Omega \times \left( \frac{d\mathbf{r'}}{dt} \right)_{\mathcal{F}}$$

Entonces simplificando tenemos que

$$\mathbf{a} = \mathbf{A} + \left( \frac{d\mathbf{v'}}{dt} \right)_{\mathcal{F}} + \dot{\Omega} \times \mathbf{r'} + \Omega \times \left( \frac{d\mathbf{r'}}{dt} \right)_{\mathcal{F}}$$

Recordamos que $\left( \frac{d\mathbf{r'}}{dt} \right)_{\mathcal{F}} = \mathbf{v'} + \Omega\times \mathbf{r'}$ y entonces $\left( \frac{d\mathbf{v'}}{dt} \right)_{\mathcal{F}} = \mathbf{a'} + \Omega\times \mathbf{v'}$ por lo tanto:

$$\mathbf{a} = \mathbf{A} + \mathbf{a'} + \Omega \times \mathbf{v'} + \Omega \times \mathbf{v'} + \dot{\Omega} \times \mathbf{r'} + \Omega \times (\Omega \times \mathbf{r'})$$

Simplificando los términos que se repiten, obtenemos:

$$\mathbf{a} = \mathbf{A} + \mathbf{a'} + 2\Omega \times \mathbf{v'} + \dot{\Omega} \times \mathbf{r'} + \Omega \times (\Omega \times \mathbf{r'})$$

La expresión simplificada de la aceleración en un sistema de referencia rotativo que obtuvimos es:

$$\mathbf{a} = \mathbf{A} + \mathbf{a'} + 2\Omega \times \mathbf{v'} + \dot{\Omega} \times \mathbf{r'} + \Omega \times (\Omega \times \mathbf{r'})$$

Y en el problema circular restringido de tres cuerpos, consideramos tres masas: $m_1$, $m_2$, y $m_3$. Aquí, recordamos que $m_1$ y $m_2$ son dos masas grandes (por ejemplo, dos estrellas o un planeta y su luna), y $m_3$ es una masa significativamente menor (como un asteroide o una nave espacial) que no afecta gravitacionalmente a los otros dos cuerpos. Como ya habíamos hablado más o menos, este sistema se analiza comúnmente en un marco de referencia en rotación, donde $m_1$ y $m_2$ están fijos.

Ahora, pensemos en cada término para nuestro problema.

1. $\mathbf{A}$ - Aceleración del origen del sistema de referencia:

   • En este marco, $m_1$ y $m_2$ están en reposo por definición. Por tanto, el origen del sistema de referencia no tiene aceleración respecto a un sistema inercial, entonces $\mathbf{A} = 0$.

2. $\mathbf{a'}$ - Aceleración de $m_3$ relativa al sistema de referencia:

   • Este término no se hace cero y es crítico para el análisis. Representa la aceleración de $m_3$ debida principalmente a las fuerzas gravitacionales de $m_1$ y $m_2$, ajustada por la dinámica del marco rotatorio.

3. $2\Omega \times \mathbf{v'}$ - Aceleración de Coriolis:

   • Este término tampoco es cero. Afecta a la trayectoria de $m_3$ dentro del marco rotatorio debido a su velocidad relativa $\mathbf{v'}$ en el sistema.

4. $\dot{\Omega} \times \mathbf{r'}$ - Aceleración de Euler:

   • Dado que el marco de referencia rota con una velocidad angular constante (la misma velocidad angular de la órbita mutua de $m_1$ y $m_2$, $\dot{\Omega}$ es cero. Por lo tanto, no hay aceleración de Euler en este problema.

5. $\Omega \times (\Omega \times \mathbf{r'})$ - Aceleración centrífuga:

   • Este término no es cero. Pues nos dice la fuerza centrífuga experimentada por $m_3$ debido a su posición relativa en el marco rotatorio. Sabemos que este efecto nos dice cómo $m_3$ es empujado hacia afuera desde el eje de rotación.

Entonces, nos quedaría que:

$$\mathbf{a} = \mathbf{a'} + 2\Omega \times \mathbf{v'} + \Omega \times (\Omega \times \mathbf{r'})$$

Por segunda ley de Newton tenemos que:

$$\mathbf{a} = \mathbf{a'} + 2\Omega \times \mathbf{v'} + \Omega \times (\Omega \times \mathbf{r'}) = \frac{\mathbf{F}}{m_{3}}$$

Pensando en que estamos describiendo la dinámica del tercer cuerpo $m_{3}$ y como $\mathbf{F} = -\nabla U$ entonces:

$$\mathbf{a} = \mathbf{a'} + 2\Omega \times \mathbf{v'} + \Omega \times (\Omega \times \mathbf{r'}) = -\frac{\nabla U}{m_{3}}$$ $$\mathbf{a'} + 2\Omega \times \mathbf{v'} = -\frac{\nabla U}{m_{3}}- \Omega \times (\Omega \times \mathbf{r'})$$

Pero recordando que $\vec{A} \times (\vec{B} \times \vec{C}) = (\vec{A} \cdot \vec{C}) \vec{B} - (\vec{A} \cdot \vec{B}) \vec{C}$

Entonces llegamos a que $\Omega \times (\Omega \times \mathbf{r'}) = (\Omega \cdot \mathbf{r'}) \Omega - (\Omega \cdot \Omega) \mathbf{r'}$, pero en la dinámica de rotación $\Omega$ y $\mathbf{r'}$ son perpendiculares, entonces $\Omega \cdot \mathbf{r'} = 0$, por lo tanto:

$$\Omega \times (\Omega \times \mathbf{r'}) = - (\Omega \cdot \Omega) \mathbf{r'} = -|\Omega|^{2}\mathbf{r'} = -\Omega^{2}\mathbf{r'}$$

Entonces, tendríamos que:

$$\mathbf{a'} + 2\Omega \times \mathbf{v'} = -\frac{\nabla U}{m_{3}} + \Omega^{2}\mathbf{r'}$$

Para meter este último término dentro del gradiente tendríamos que integrarlo, por lo que tenemos:

$$\mathbf{a'} + 2\Omega \times \mathbf{v'} = -\nabla\left( \frac{U}{m_{3}} - \frac{1}{2}\Omega^{2}(\mathbf{r'})^{2} \right)$$

Ahora, $U(\mathbf{r})$ representa el potencial gravitacional que actúa sobre $m_{3}$ debido a $m_{1}$ y $m_{2}$.

En donde para este caso tendríamos que:

$$U(\mathbf{r}) = -\frac{Gm_{1}m_{3}}{|\mathbf{r}-\mathbf{r_{1}}|}-\frac{Gm_{2}m_{3}}{|\mathbf{r}-\mathbf{r_{1}}|}$$

Sustituyendo esta expresión tenemos que:

$$\mathbf{a'} + 2\Omega \times \mathbf{v'} = -\nabla\left( -\frac{Gm_{1}}{|\mathbf{r}-\mathbf{r_{1}}|} - \frac{Gm_{2}}{|\mathbf{r}-\mathbf{r_{2}}|} - \frac{1}{2}\Omega^{2}(\mathbf{r'})^{2} \right)$$

---

Ahora veamos un simple esquema de nuestro problema. [dibujo]

Donde $\mathbf{r} = (x,y,z)$ es la distancia de $m_{3}$ al centro de gravedad de $m_{1}$ y $m_{2}$.

Ahora, para simplificar, podemos hacer que:

$$\begin{align*} m_{1} + m_{2} &= 1 \\ R = \mathbf{r_{2}} - \mathbf{r_{1}} &= 1 \\ \Omega &=1 \\ G &= 1 \end{align*}$$

Sabemos que la fórmula general para el centro de masa entre dos puntos masivos es:

$$CM = \frac{m_{1}\mathbf{r_{1}}+m_{2}\mathbf{r_{2}}}{m_{1}+m_{2}}$$

Que se simplifica a:

$$CM = m_{1}\mathbf{r_{1}}+m_{2}\mathbf{r_{2}}$$

Si alineamos el centro de masa en el origen, entonces llegamos a que: $m_{1}\mathbf{r_{1}} = -m_{2}\mathbf{r_{2}}$ Y por lo tanto:

$$r_{1} = -\frac{m_{2}\mathbf{r}_{2}}{m_{1}} \tag{$\alpha$}$$

Si ahora definimos $\mu = m_{2}$, usando que $m_{1} + m_{2} = 1$ entonces $m_{1}+\mu=1 \rightarrow m_{1}=1-\mu$. Sustituyendo en la ecuación ($\alpha$) que teníamos, nos queda que:

$$r_{1} = -\frac{m_{2}\mathbf{r}_{2}}{m_{1}} = -\frac{\mu}{1-\mu}\mathbf{r_{2}}$$

Pero recordando que $r_{2} - r_{1} = 1$, entonces:

$$r_{2} + \frac{\mu}{1-\mu}r_{2} = 1$$

Simplificando llegamos a que:

$$\begin{align*} r_{2}\left( 1+\frac{\mu}{1-\mu} \right) &= 1 \\ r_{2}\left( \frac{1-\mu+\mu}{1-\mu} \right) &= 1 \\ r_{2}\left( \frac{1}{1-\mu} \right) &= 1 \\ \therefore r_{2} = 1-\mu \end{align*}$$

Y entonces:

$$r_{1} = -\frac{m_{2}\mathbf{r}_{2}}{m_{1}} = -\frac{\mu}{1-\mu}\mathbf{r_{2}} = -\frac{\mu}{1-\mu}(1-\mu)=-\mu$$

Por lo tanto concluímos que:

$$\begin{align*} r_{1} = -\mu = -m_{2} \\ r_{2} = 1-\mu=m_{1} \end{align*}$$

Y entonces, habíamos definido el siguiente potencial efectivo:

$$U(r) = \left( -\frac{Gm_{1}}{|\mathbf{r}-\mathbf{r_{1}}|} - \frac{Gm_{2}}{|\mathbf{r}-\mathbf{r_{2}}|} - \frac{1}{2}\Omega^{2}r^{2} \right)$$

Y ya vimos que $m_{1}$ está en $r_{1}=(-\mu, 0)$ y $m_{2}$ está en $r_{2}=(1-\mu, 0)$.

Dado que $m_1$ está en $r_1 = (-\mu, 0)$ y $m_2$ está en $r_2 = (1-\mu, 0)$, podemos reescribir $U(r)$ en términos de $x, y, z$:

1. Distancia entre $\mathbf{r}$ y $\mathbf{r_1}$:

$$|\mathbf{r} - \mathbf{r_1}| = \sqrt{(x + \mu)^2 + y^2}$$

2. Distancia entre $\mathbf{r}$ y $\mathbf{r_2}$:

$$|\mathbf{r} - \mathbf{r_2}| = \sqrt{(x - (1-\mu))^2 + y^2}$$

Sustituyendo estas expresiones en el potencial efectivo $U(r)$:

$$U(x, y) = -\frac{1-\mu}{\sqrt{(x + \mu)^2 + y^2}} - \frac{\mu}{\sqrt{(x - (1-\mu))^2 + y^2}} - \frac{1}{2}(x^2 + y^2)$$

Para obtener las ecuaciones de movimiento a partir de la ecuación de aceleración dada, recordamos que

$$\mathbf{a'} + 2\Omega \times \mathbf{v'} =\ddot{\mathbf{r}} + 2\mathbf{\Omega} \times \dot{\mathbf{r}} = - \nabla U(\mathbf{r}),$$

Primero vemos que el término de Coriolis $2\mathbf{\Omega} \times \dot{\mathbf{r}}$ en coordenadas cartesianas se expresa como:

$$2\mathbf{\Omega} \times \dot{\mathbf{r}} = 2 \begin{pmatrix} 0 \\ 0 \\ \Omega \end{pmatrix} \times \begin{pmatrix} \dot{x} \\ \dot{y} \\ \dot{z} \end{pmatrix} = 2\Omega \begin{pmatrix} -\dot{y} \\ \dot{x} \\ 0 \end{pmatrix}.$$

Y como $\Omega =1$ Por lo tanto, en componentes, la ecuación de movimiento se descompone en:

$$\ddot{x} - 2 \dot{y} = -\frac{\partial U}{\partial x},$$ $$\ddot{y} + 2\dot{x} = -\frac{\partial U}{\partial y},$$ $$\ddot{z} = -\frac{\partial U}{\partial z}.$$

Calculando el gradiente del potencial

El potencial $U(x, y)$ es:

$$U(x, y) = -\frac{1 - \mu}{\sqrt{(x + \mu)^2 + y^2}} - \frac{\mu}{\sqrt{(x - 1 + \mu)^2 + y^2}} - \frac{1}{2} \left(x^2 + y^2 \right).$$

Entonces, los gradientes son:

$$\frac{\partial U}{\partial x} = \frac{(1 - \mu)(x + \mu)}{\left[(x + \mu)^2 + y^2\right]^{3/2}} + \frac{\mu(x - 1 + \mu)}{\left[(x - 1 + \mu)^2 + y^2\right]^{3/2}} - x,$$ $$\frac{\partial U}{\partial y} = \frac{(1 - \mu)y}{\left[(x + \mu)^2 + y^2\right]^{3/2}} + \frac{\mu y}{\left[(x - 1 + \mu)^2 + y^2\right]^{3/2}} - y.$$

Sustituimos estos gradientes en las ecuaciones de movimiento:

Ecuación para $x$:

$$\ddot{x} - 2 \dot{y} = -\left[ \frac{(1 - \mu)(x + \mu)}{\left[(x + \mu)^2 + y^2\right]^{3/2}} + \frac{\mu(x - 1 + \mu)}{\left[(x - 1 + \mu)^2 + y^2\right]^{3/2}} - x \right],$$ $$\ddot{x} = 2 \dot{y} - \frac{(1 - \mu)(x + \mu)}{\left[(x + \mu)^2 + y^2\right]^{3/2}} - \frac{\mu(x - 1 + \mu)}{\left[(x - 1 + \mu)^2 + y^2\right]^{3/2}} + x.$$

Ecuación para $y$:

$$\ddot{y} + 2 \dot{x} = -\left[ \frac{(1 - \mu)y}{\left[(x + \mu)^2 + y^2\right]^{3/2}} + \frac{\mu y}{\left[(x - 1 + \mu)^2 + y^2\right]^{3/2}} - y \right],$$ $$\ddot{y} = -2 \dot{x} - \frac{(1 - \mu)y}{\left[(x + \mu)^2 + y^2\right]^{3/2}} - \frac{\mu y}{\left[(x - 1 + \mu)^2 + y^2\right]^{3/2}} + y.$$

Ecuación para $z$:

Dado que el potencial $V(x, y)$ no depende de $z$, la ecuación en $z$ es simplemente:

$$\ddot{z} = 0.$$

Por lo tanto:

$$\ddot{x} = 2 \dot{y} - \frac{(1 - \mu)(x + \mu)}{\left[(x + \mu)^2 + y^2\right]^{3/2}} - \frac{\mu(x - 1 + \mu)}{\left[(x - 1 + \mu)^2 + y^2\right]^{3/2}} + x,$$ $$\ddot{y} = -2 \dot{x} - \frac{(1 - \mu)y}{\left[(x + \mu)^2 + y^2\right]^{3/2}} - \frac{\mu y}{\left[(x - 1 + \mu)^2 + y^2\right]^{3/2}} + y,$$ $$\ddot{z} = 0.$$

Para resolver las ecuaciones de movimiento necesitamos convertirlas a un sistema de primer orden. Entonces definimos:

$$v_x = \dot{x}, \quad v_y = \dot{y}, \quad v_z = \dot{z}$$

entonces las aceleraciones se escriben como derivadas de las velocidades:

$$\begin{aligned} \dot{v}_x &= \ddot{x}, \\ \dot{v}_y &= \ddot{y}, \\ \dot{v}_z &= \ddot{z}. \end{aligned}$$

Ahora, sustituimos las ecuaciones de segundo grado para $\ddot{x}$, $\ddot{y}$ y $\ddot{z}$ obtenidas anteriormente:

Ecuación para $\ddot{x}$:

$$\ddot{x} = 2 v_y - \frac{(1 - \mu)(x + \mu)}{\left[(x + \mu)^2 + y^2\right]^{3/2}} - \frac{\mu(x - 1 + \mu)}{\left[(x - 1 + \mu)^2 + y^2\right]^{3/2}} + x$$

Se convierte en:

$$\dot{v}_x = 2 v_y - \frac{(1 - \mu)(x + \mu)}{\left[(x + \mu)^2 + y^2\right]^{3/2}} - \frac{\mu(x - 1 + \mu)}{\left[(x - 1 + \mu)^2 + y^2\right]^{3/2}} + x$$

Ecuación para $\ddot{y}$:

$$\ddot{y} = -2 v_x - \frac{(1 - \mu)y}{\left[(x + \mu)^2 + y^2\right]^{3/2}} - \frac{\mu y}{\left[(x - 1 + \mu)^2 + y^2\right]^{3/2}} + y$$

Se convierte en:

$$\dot{v}_y = -2 v_x - \frac{(1 - \mu)y}{\left[(x + \mu)^2 + y^2\right]^{3/2}} - \frac{\mu y}{\left[(x - 1 + \mu)^2 + y^2\right]^{3/2}} + y$$

Ecuación para $\ddot{z}$:

$$\ddot{z} = 0$$

Se convierte en:

$$\dot{v}_z = 0$$

Sistema de ecuaciones de primer grado

El sistema de ecuaciones de primer grado que describe el movimiento del cuerpo en el plano $xy$ es:

$$\begin{aligned} \dot{x} &= v_x, \\ \dot{y} &= v_y, \\ \dot{v}_x &= 2 v_y - \frac{(1 - \mu)(x + \mu)}{\left[(x + \mu)^2 + y^2\right]^{3/2}} - \frac{\mu(x - 1 + \mu)}{\left[(x - 1 + \mu)^2 + y^2\right]^{3/2}} + x, \\ \dot{v}_y &= -2 v_x - \frac{(1 - \mu)y}{\left[(x + \mu)^2 + y^2\right]^{3/2}} - \frac{\mu y}{\left[(x - 1 + \mu)^2 + y^2\right]^{3/2}} + y, \\ \end{aligned}$$