Condiciones iniciales del problema de tres cuerpos

¿Qué son los Puntos de Lagrange?

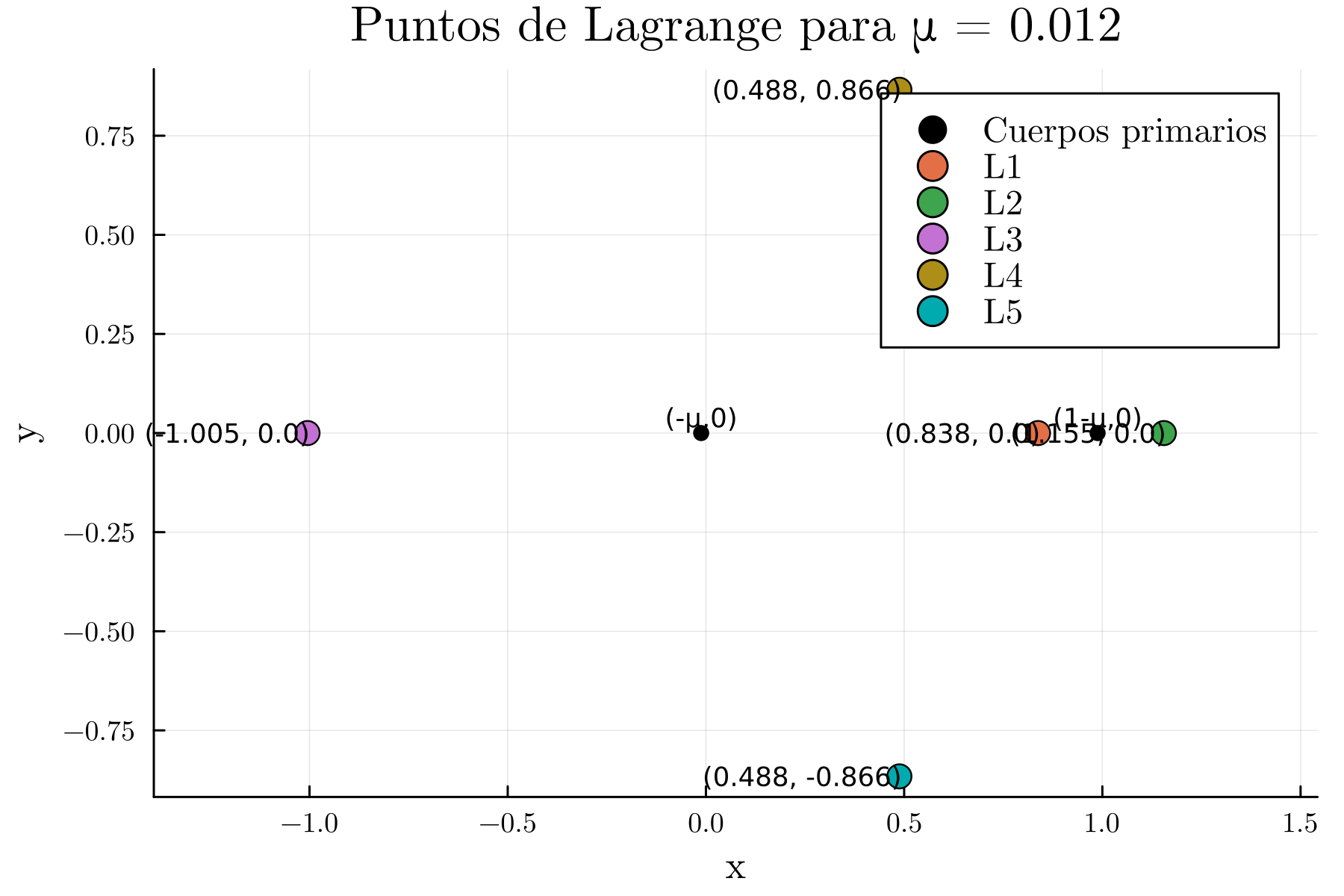
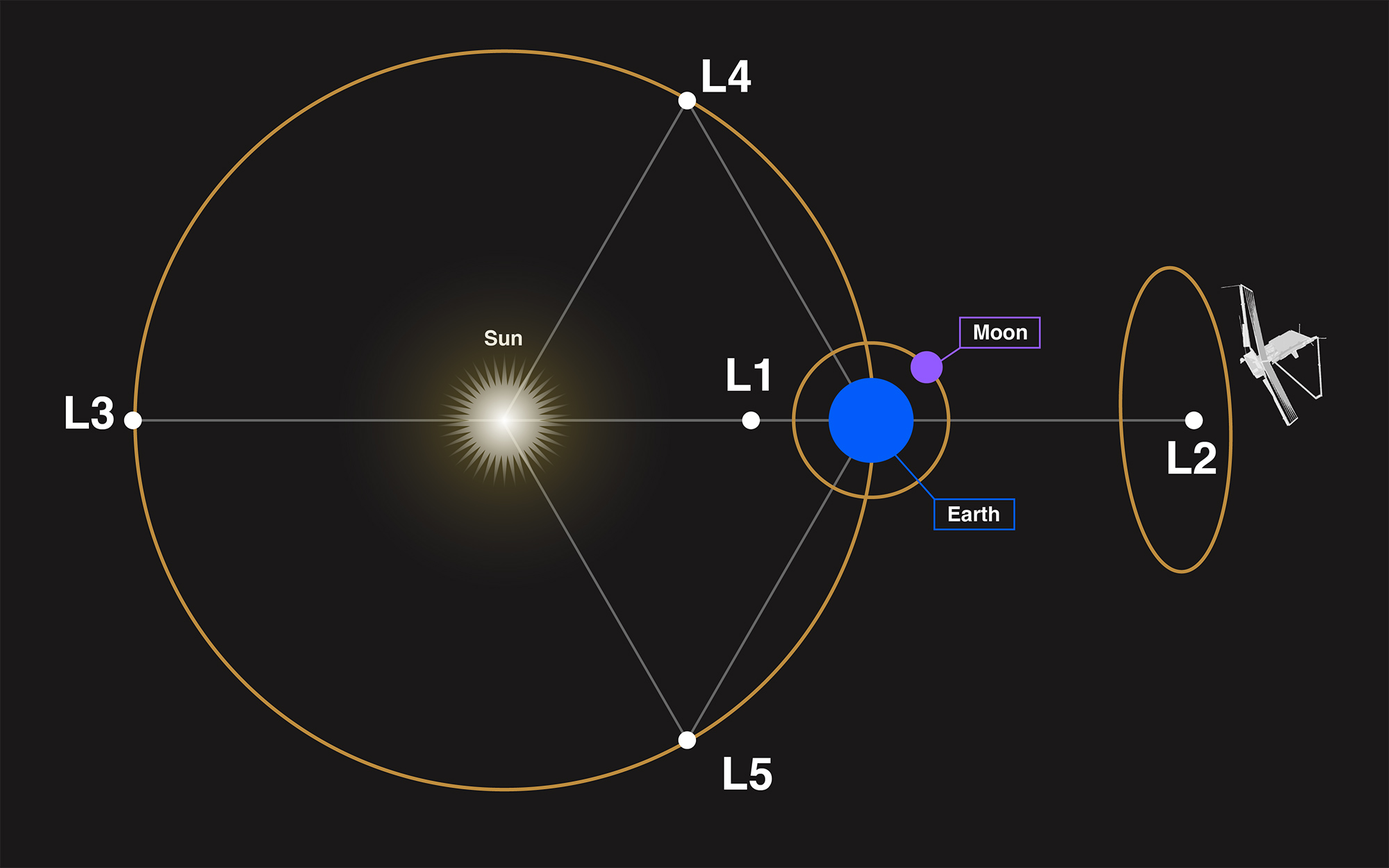
Los puntos de Lagrange son cinco posiciones específicas en el espacio donde las fuerzas gravitacionales combinadas de los dos cuerpos principales y la fuerza centrífuga experimentada por el tercer cuerpo se equilibran perfectamente. Estos puntos se denominan $L_1, L_2, L_3, L_4$ y $L_5$ :

$L_1$ , $L_2$ y $L_3$ se encuentran en la línea que une a los dos cuerpos principales.
$L_4$ y $L_5$ forman un triángulo equilátero con los cuerpos principales y están situados 60 grados adelante y detrás del cuerpo menor en su órbita.

Estos puntos son de particular interés no solo por su estabilidad dinámica, sino también por sus aplicaciones prácticas en la planificación de misiones espaciales, donde se utilizan para posicionar satélites.

lagra

¿Por qué nos interesan para nuestras condiciones iniciales?

Porque nos permite explorar la estabilidad y la dinámica local de las trayectorias que se desarrollan en su proximidad. Al ser puntos de equilibrio, pequeñas perturbaciones alrededor de ellos pueden dar lugar a comportamientos dinámicos complejos, incluyendo órbitas periódicas, cuasi-periódicas e incluso movimientos caóticos.

Para calcular los puntos de Lagrange se procedió de la siguiente forma:

Se define una función que representa el sistema de ecuaciones no lineales que describen las condiciones de equilibrio en el campo gravitacional combinado de los dos cuerpos principales. Esta función evalúa las fuerzas gravitacionales y la fuerza centrífuga para determinar si están balanceadas.
Se seleccionan posiciones iniciales cercanas a las ubicaciones teóricas esperadas de los puntos de Lagrange. Estas posiciones sirven como punto de partida para el método numérico de resolución.
Se utiliza un algoritmo de resolución de ecuaciones no lineales, como el proporcionado por el paquete NLsolve en Julia, para iterativamente encontrar las posiciones exactas de los puntos de Lagrange que satisfacen las condiciones de equilibrio.
Una vez obtenidas las soluciones numéricas, se comparan con las aproximaciones teóricas para evaluar la precisión del método y entender las posibles fuentes de error.

Explicación del Código

using NLsolve
using LinearAlgebra

# valores de μ a considerar
μvals = 0.001:0.001:0.5
nμvals = length(μvals)

# Inicialización de una matriz para almacenar las posiciones de los puntos de Lagrange
# Cada fila corresponde a un valor de μ y las columnas almacenan las coordenadas (x, y) de los cinco puntos
p_lagrange = zeros(Float64, nμvals, 10)

# función que representa el sistema de ecuaciones no lineales
function evalF!(F, X, μ)
    x, y = X
    F[1] = x - (1 - μ)*(x + μ)/((x + μ)^2 + y^2)^(3/2) - μ*(x + μ - 1)/((x + μ - 1)^2 + y^2)^(3/2)
    F[2] = y - (1 - μ)*y/((x + μ)^2 + y^2)^(3/2) - μ*y/((x + μ - 1)^2 + y^2)^(3/2)
end

# posiciones iniciales aproximadas para los cinco puntos de Lagrange
initial_positions = [
    [0.0, 0.0],         # Aproximación para L1
    [1.0, 0.0],         # Aproximación para L2
    [-1.0, 0.0],        # Aproximación para L3
    [0.0, 1.0],         # Aproximación para L4
    [0.0, -1.0]         # Aproximación para L5
]

# Iteración sobre cada valor de μ
for (i, μ) in enumerate(μvals)
    for (j, pos) in enumerate(initial_positions)
        # Resolución del sistema de ecuaciones usando NLsolve
        result = nlsolve((F, X) -> evalF!(F, X, μ), pos, autodiff=:forward)
        # Almacenamiento de la solución en la matriz p_lagrange
        p_lagrange[i, (2j-1):(2j)] = result.zero
    end
end

Comparación con Aproximaciones Teóricas y Análisis de Error

Para validar la precisión de las soluciones numéricas obtenidas, es esencial compararlas con las aproximaciones teóricas de los puntos de Lagrange. Estas aproximaciones proporcionan valores cercanos a las posiciones reales de los puntos y sirven como referencia para medir los errores en las soluciones numéricas.

# aproximaciones teóricas para los cinco puntos de Lagrange
theoretical_approximations = [
    μ -> 1 - ∛(μ/3),          # Aproximación para L1
    μ -> 0,                    # Aproximación para L2 (simplificada)
    μ -> 1 + ∛(μ/3),          # Aproximación para L3
    μ -> 0,                    # Aproximación para L4 (simplificada)
    μ -> -1 - 5μ/12,           # Aproximación para L5 (simplificada)
    μ -> 0,                    # Aproximación para L4 en y
    μ -> 1/2 - μ,              # Aproximación para L4 en x
    μ -> √3/2,                 # Aproximación para L4 en y
    μ -> 1/2 - μ,              # Aproximación para L5 en x
    μ -> -√3/2                 # Aproximación para L5 en y
]

# matriz para almacenar los errores
errors = zeros(Float64, length(μvals), 10)

# errores absolutos entre las soluciones numéricas y las teóricas
for idx in 1:10
    errors[:, idx] = abs.(p_lagrange[:, idx] .- [theoretical_approximations[idx](μ) for μ in μvals])
end

Exploración de un Nuevo Valor de $\mu$

Para profundizar en el comportamiento de los puntos de Lagrange, podemos analizar casos específicos. Por ejemplo, consideremos el caso donde $\mu = \frac{1}{81}$ .

nuevo_μ = 1/81
nuevo = zeros(Float64, 10)

for (j, pos) in enumerate(initial_positions)
    result = nlsolve((F, X) -> evalF!(F, X, nuevo_μ), pos, autodiff=:forward)
    nuevo[(2j-1):(2j)] = result.zero
end

println("Nuevo μ = $nuevo_μ:$(nuevo)")

pltlagr