❉ Hamiltoniano y Curvas de Nivel Cero ❉

Introducción al Enfoque Hamiltoniano

Para simplificar el análisis del problema, realizamos una transformación de coordenadas entre el sistema de referencia sideral $(X, Y)$ y el sistema sinódico $(x, y)$, mediante una rotación dependiente del tiempo $\omega$:

Consideremos la transformación entre coordenadas siderales $(X, Y)$ y coordenadas sinódicas $(x, y)$, que es una vil rotación dependiente del tiempo:

$$\begin{aligned} X &= x \cos(\omega t) - y \sin(\omega t), \\ Y &= x \sin(\omega t) + y \cos(\omega t), \end{aligned}$$

$\omega$ es la velocidad angular de rotación del sistema de referencia sinódico.

Función Generadora de la Transformación Canónica

Definimos la función generadora $W$ en términos de los nuevos momentos $(P_X, P_Y)$ y las viejas coordenadas $(x, y)$:

$$W =P_{X}X + P_{Y}Y$$ $$W = P_X \left( x \cos(\omega t) - y \sin(\omega t) \right) + P_Y \left( x \sin(\omega t) + y \cos(\omega t) \right).$$

A partir de la función generadora, obtenemos las siguientes relaciones canónicas:

$$\begin{aligned} X &= \frac{\partial W}{\partial P_X} = x \cos(\omega t) - y \sin(\omega t), \\ Y &= \frac{\partial W}{\partial P_Y} = x \sin(\omega t) + y \cos(\omega t), \\ p_x &= \frac{\partial W}{\partial x} = P_X \cos(\omega t) + P_Y \sin(\omega t), \\ p_y &= \frac{\partial W}{\partial y} = -P_X \sin(\omega t) + P_Y \cos(\omega t). \end{aligned}$$

Cálculo de $\frac{dW}{dt}$

Calculamos la derivada total de $W$ respecto al tiempo $t$:

$$W = P_X \left[ x \cos(\omega t) - y \sin(\omega t) \right] + P_Y \left[ x \sin(\omega t) + y \cos(\omega t) \right]$$ $$\frac{d}{dt} \left( P_X \left[ x \cos(\omega t) - y \sin(\omega t) \right] \right) = P_X \left[ -x \omega \sin(\omega t) - y \omega \cos(\omega t) \right]$$ $$\frac{d}{dt} \left( P_Y \left[ x \sin(\omega t) + y \cos(\omega t) \right] \right) = P_Y \left[ x \omega \cos(\omega t) - y \omega \sin(\omega t) \right]$$ $$\frac{dW}{dt} = P_X \left[ -x \omega \sin(\omega t) - y \omega \cos(\omega t) \right] + P_Y \left[ x \omega \cos(\omega t) - y \omega \sin(\omega t) \right]$$ $$\frac{dW}{dt} = \omega \left( -P_X x \sin(\omega t) - P_X y \cos(\omega t) + P_Y x \cos(\omega t) - P_Y y \sin(\omega t) \right)$$ $$\frac{dW}{dt} = -\omega P_X \left( x \sin(\omega t) + y \cos(\omega t) \right) + \omega P_Y \left( x \cos(\omega t) - y \sin(\omega t) \right) = \omega (Y P_X - X P_Y).$$

El nuevo Hamiltoniano $J$ lo obtenemos de la forma:

$$J = H + \frac{dW}{dt},$$

donde $H$ es el Hamiltoniano en coordenadas siderales.

Expresión del Hamiltoniano Completo

Teníamos que el potencial efectivo era:

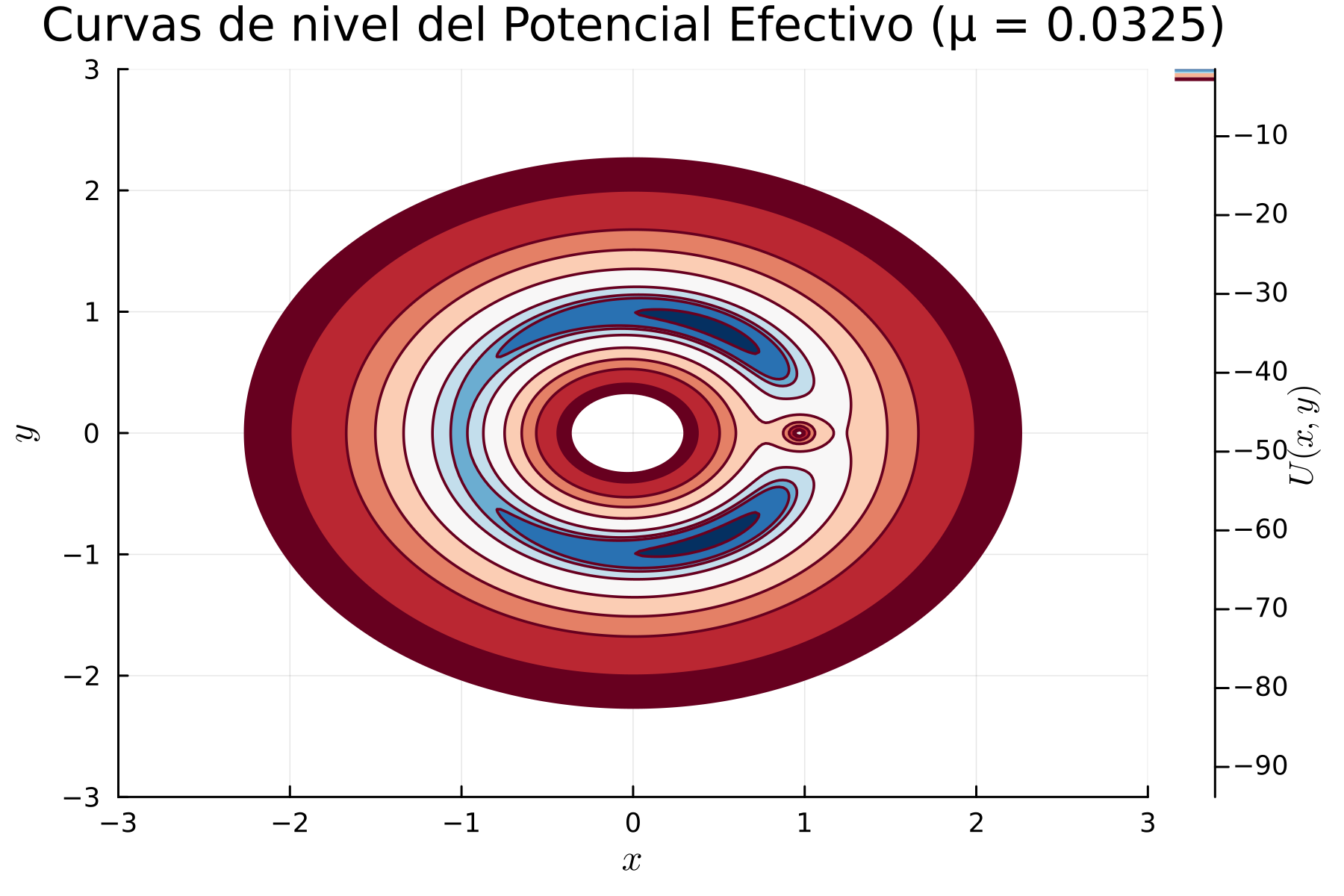
$$U(x, y) = -\frac{1-\mu}{\sqrt{(x + \mu)^2 + y^2}} - \frac{\mu}{\sqrt{(x - (1-\mu))^2 + y^2}}$$

La energía cinética es:

$$T = \frac{1}{2}(p_x^2 + p_y^2).$$

Entonces, el Hamiltoniano completo sería:

$$H(X, Y, P_X, P_Y) = \frac{1}{2}(P_X^2 + P_Y^2) - \frac{1-\mu}{\sqrt{(X + \mu)^2 + Y^2}} - \frac{\mu}{\sqrt{(X - (1-\mu))^2 + Y^2}}$$

Sustituyendo $H$ y $\frac{dW}{dt}$ en la expresión de $J$, obtenemos:

$$\begin{align*} J &= H + \frac{dW}{dt} \\ &= \frac{1}{2}(P_X^2 + P_Y^2) - \frac{1-\mu}{\sqrt{(X + \mu)^2 + Y^2}} - \frac{\mu}{\sqrt{(X - (1-\mu))^2 + Y^2}} + \omega (Y P_X - X P_Y). \end{align*}$$

Utilizando las relaciones de transformación:

$$\begin{aligned} X &= x \cos(\omega t) - y \sin(\omega t), \\ Y &= x \sin(\omega t) + y \cos(\omega t), \\ P_X &= p_x \cos(\omega t) + p_y \sin(\omega t), \\ P_Y &= -p_x \sin(\omega t) + p_y \cos(\omega t), \end{aligned}$$ $$J(x, y, p_x, p_y) = \frac{1}{2}(p_x^2 + p_y^2) - \frac{1-\mu}{\sqrt{(x + \mu)^2 + y^2}} - \frac{\mu}{\sqrt{(x - (1-\mu))^2 + y^2}} + \omega (y p_x - x p_y).$$

Aplicando las ecuaciones de Hamilton al Hamiltoniano $J$, obtenemos las ecuaciones de movimiento:

$$\begin{aligned} \dot{x} &= \frac{\partial J}{\partial p_x} = p_x + \omega y, \\ \dot{y} &= \frac{\partial J}{\partial p_y} = p_y - \omega x, \\ \dot{p_x} &= -\frac{\partial J}{\partial x} = \frac{(1-\mu)(x+\mu)}{[(x+\mu)^2 + y^2]^{3/2}} + \frac{\mu(x-(1-\mu))}{[(x-(1-\mu))^2 + y^2]^{3/2}} + \omega p_y, \\ \dot{p_y} &= -\frac{\partial J}{\partial y} = -\frac{(1-\mu)y}{[(x+\mu)^2 + y^2]^{3/2}} - \frac{\mu y}{[(x-(1-\mu))^2 + y^2]^{3/2}} - \omega p_x. \end{aligned}$$

Estas ecuaciones describen la evolución temporal de las posiciones y los momentos del sistema en el marco sinódico.

Implementación en Julia: Curvas de Nivel Cero

# Parámetro de masa 
mu = 0.0325

# Función del potencial efectivo
@inline function U(x, y, mu)
    r1 = sqrt((x + mu)^2 + y^2)
    r2 = sqrt((x - (1 - mu))^2 + y^2)
    return -(1 - mu) / r1 - mu / r2 - 0.5(x^2 + y^2)
end

# malla
x = LinRange(-3, 3, 300)
y = LinRange(-3, 3, 300)
U_values = [U(xi, yi, mu) for yi in y, xi in x]

# niveles de contorno
levels = [
    -3.0, -2.5, -2.0, -1.8, -1.65, -1.55, -1.52, -1.51, -1.49, -1.48
]

# gráfico de las curvas de nivel
p = contour(x, y, U_values,
    levels = levels,
    color = :RdBu,
    linewidth = 1.2,
    fill = true,
    xlabel = L"x",
    ylabel = L"y",
    title = "Curvas de nivel del Potencial Efectivo (μ = 0.0325)",
    colorbar_title = L"U(x,y)",
    background_color = :white,
    foreground_color = :black,
    colorbar_formatter = :scientific,
)

display(p)

Explicación del Código

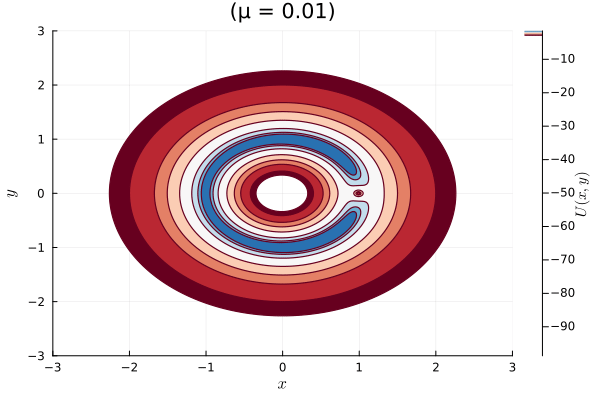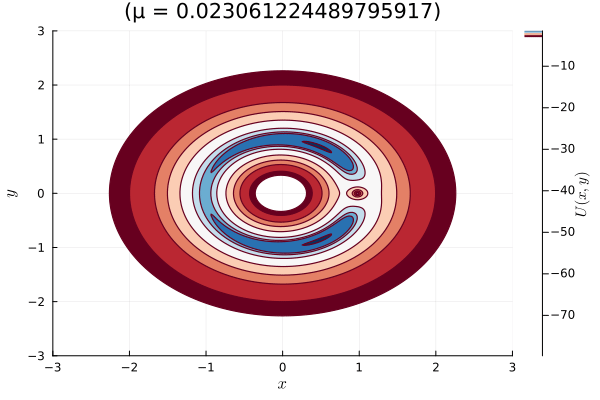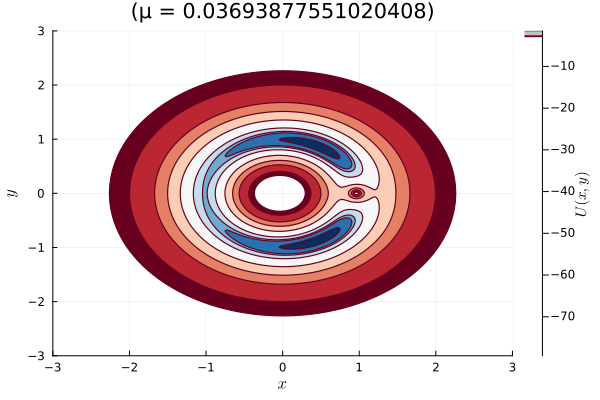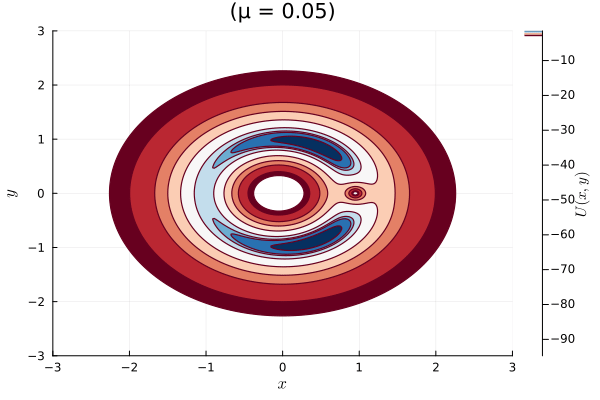
• Función U: Calcula el potencial efectivo $U(x, y)$ basado en las posiciones $x, y$ y el parámetro de masa $\mu$.

• Malla: Se crea una malla de puntos $(x, y)$ en un rango de $-3$ a $3$.

• Niveles de contorno: Se definen niveles de energía para mostrar las curvas de nivel que representan los valores de energía potencial.

mu_values = LinRange(0.01, 0.05, 50)

anim = @animate for mu in mu_values
    # Crear la malla
    x = LinRange(-3, 3, 300)
    y = LinRange(-3, 3, 300)
    U_values = [U(xi, yi, mu) for yi in y, xi in x]

    contour(
        x, y, U_values,
        levels = levels,
        color = :RdBu,
        linewidth = 1.2,
        fill = true,
        xlabel = L"x",
        ylabel = L"y",
        title = "(μ = $mu)",
        colorbar_title = L"U(x,y)",
        background_color = :white,
        foreground_color = :black,
        colorbar_formatter = :scientific
    )
end

# Guardar la animación como GIF
gif(anim, "mi_animacion.gif", fps = 10)  # Cambia los fotogramas por segundo según sea necesario

El enfoque hamiltoniano nos da una forma clara y organizada de entender el sistema de tres cuerpos en un marco de referencia que se mueve con ellos. A través de las curvas de nivel cero del potencial efectivo, podemos visualizar las áreas en el espacio donde la energía cinética del sistema se anula. Esto resulta clave para comprender cómo se mueven y mantienen estables los cuerpos en órbita.

Este análisis es fundamental para identificar zonas de equilibrio y para mapear las posibles trayectorias de cuerpos pequeños.