Introduciendo el problema de tres cuerpos

Ahora consideremos a un tercer cuerpo mucho menos masivo que los otros dos tal que: $m_{3}\ll m_{2}\leq m_{1}$. De esta forma, podemos ignorar las contribuciones dinámicas de $m_{3}$ al movimiento de $m_{1}$ y $m_{2}$, y la solución sigue siendo la misma que desarrollamos en la entrada anterior. Entonces, nos interesa únicamente describir la dinámica de $m_{3}$.

Teníamos que para dos cuerpos

$$r(\theta) = \frac{c}{1 + e \cos(\theta)}$$

donde $c = \frac{L^2}{\mu^2 \beta}$ y $e = \frac{A L^2}{\mu^2 \beta}$. Por lo que:

$$r(\theta) = \frac{\frac{L^2}{\mu^2 \beta}}{1 + e \cos(\theta)}$$

Si $e=0$ entonces:

$$r(\theta)=\frac{L^{2}}{\beta \mu^{2}}$$

lo cual es una constante. Por lo tanto, tendríamos un movimiento circular. También es la entrada anterior, vimos que $\dot{\theta}=\frac{L}{\mu r^{2}}$, entonces, sea $\dot{\theta}$ la velocidad angular y usando la ecuación de nuestro movimiento circular, tendríamos que:

$$\Omega = \frac{L}{\mu r^{2}}= \frac{\sqrt{ \beta r }}{r^{2}}=\sqrt{ \frac{\beta r}{r^{4}} } = \sqrt{ \frac{G(m_{1}+m_{2})}{r^{3}} }$$

(Recordando que en la entrada anterior habíamos definido $\beta=G(m_{1}+m_{2})$.

Para la dinámica de $m_{3}$ nos conviene establecer un marco de referencia en rotación donde $m_{1}$ y $m_{2}$ estén en reposo.

Aquí entraré demasiado en detalle en lo siguiente, pues siento que cuando vi el desarrollo de estas ecuaciones en mi clase de mecánica analítica, se omitieron algunos detalles, que está bien, pero me gustaría que (me) quedara claro todo, y como es común escuchar: hacer toda la talacha, al menos una vez en la vida.

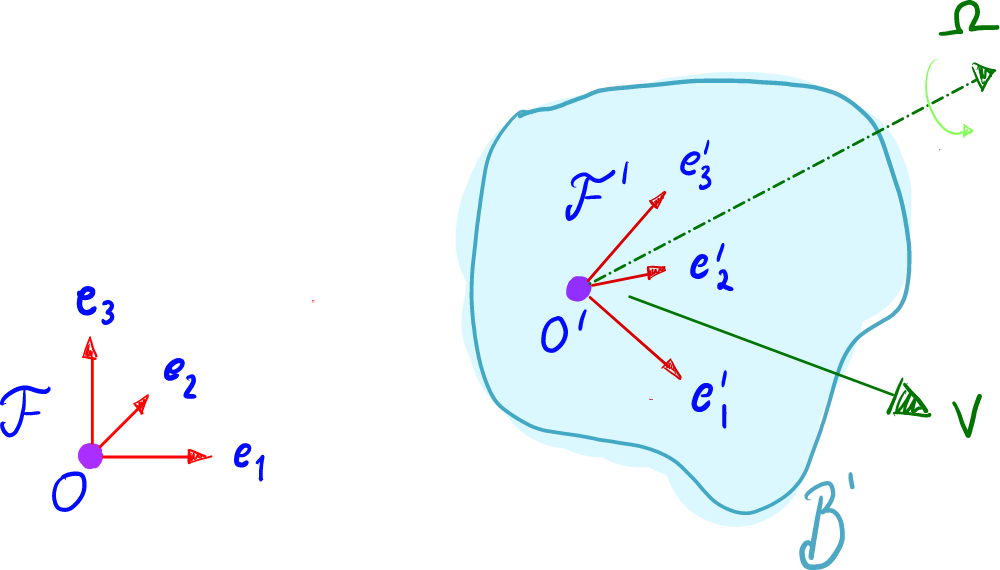
Entonces, partamos definiendo nuestro sistema inercial, es decir, nuestro sistema que estará fijo, tal que: $\mathcal{F}\equiv \left\{ O; \mathbf{e}_1, \mathbf{e}_{2}, \mathbf{e}_{3} \right\}$. Para nuestro sistema no inercial, es decir, el marco de referencia en movimiento, tenemos: $\mathcal{F}' \equiv \left\{ O'; \mathbf{e}_{1}', \mathbf{e}_{2}',\mathbf{e}_{3}' \right\}$. Como se está moviendo, entonces en un tiempo $t$ el marco de referencia $\mathcal{F}'$ tiene velocidad traslacional $\mathbf{V}$ y también, velocidad angular $\mathbf{\Omega}$ relativa al marco de referencia $\mathcal{F}$.

Para que nos sea más fácil visualizar todo esto, pensemos que el marco de referencia móvil $\mathcal{F}'$ está en un cuerpo rígido $\mathcal{B}'$. Así, podemos ver justo a $\mathbf{V}$ y $\mathbf{\Omega}$ como la velocidad traslacional y la velocidad angular del cuerpo $\mathcal{B}'$ respectivamente.

Entonces, con esto ya bien planteado, hay algo importante a tener en mente y es que:

La tasa de cambio de una cantidad vectorial medida en el marco 𝓕 es, de forma general, diferente que la tasa de cambio de la misma cantidad pero medida en el marco 𝓕'.

Para ver por qué cambian, supongamos una cantidad vectorial $\mathbf{u}(t)$. ¿Por qué cambia dependiendo si lo mido en un lado o en otro?

Veamos, si estamos en la base del sistema inercial, tendríamos que

$$\mathbf{u}=u_{1}\mathbf{e}_{1}+u_{2}\mathbf{e}_{2}+u_{3}\mathbf{e}_{3}$$

y en la base del sistema no inercial, tendríamos que

$$\mathbf{u}=u_{1}'\mathbf{e}'_{1}+u_{2}'\mathbf{e}'_{2}+u_{3}'\mathbf{e}'_{3}$$

aquí, en general, $\left\{ u_{1},u_{2},u_{3} \right\}$ y $\left\{ u_{1}', u_{2}',u_{3}' \right\}$ son funciones del tiempo.

Entonces, en la tasa de cambio de $\mathbf{u}$ en el marco $\mathcal{F}$, los vectores base $\left\{ \mathbf{e}_1, \mathbf{e}_{2}, \mathbf{e}_{3} \right\}$, son por definición constantes, por lo que

$$\left( \frac{d\mathbf{u}}{dt} \right)_{\mathcal{F}} = \dot{u}_{1}\mathbf{e}_{1}+\dot{u}_{2}\mathbf{e}_{2}+\dot{u}_{3}\mathbf{e}_{3}$$

Pero la tasa de cambio de $\mathbf{u}$ en $\mathcal{F}'$, con los vectores base $\left\{ \mathbf{e}'_1, \mathbf{e}'_{2}, \mathbf{e}'_{3} \right\}$ que son, por definición también constantes en este marco, tenemos que

$$\left( \frac{d\mathbf{u}}{dt} \right)_{\mathcal{F}'} = \dot{u}'_{1}\mathbf{e}'_{1}+\dot{u}'_{2}\mathbf{e}'_{2}+\dot{u}'_{3}\mathbf{e}'_{3}$$

Aquí en principio, no parecería tan claro, o al menos para mí, por qué las dos expresiones anteriores no son iguales. Algo que siempre tengo en mente cuando no estoy viendo algo claro es pensar en el caso más simple. Por lo que consideremos el caso en que $\mathbf{u}$ es constante en $\mathcal{F}'$. Entonces, tendríamos que $\left( \frac{d\mathbf{u}}{dt} \right)_{\mathcal{F}'}=0$, sin embargo, es claro que el movimiento de $\mathcal{F}'$ relativo a $\mathcal{F}$ nos dice que claramente $\mathbf{u}$ no será constante en $\mathcal{F}$ $u$, y por lo tanto, $\left( \frac{d\mathbf{u}}{dt} \right)_{\mathcal{F}}\neq{0}$.

Por comodidad y por convención, nos referimos al valor que medimos desde $\mathcal{F}$ como el valor verdadero y al que medimos desde $\mathcal{F}'$ como el valor aparente.