❉ Jet Transport para el Problema de Tres Cuerpos ❉

¿Qué es el Jet Transport?

Aunque ya se habló mas en detalle de la técnica aquí. Rápidamente, Jet Transport es una técnica que extiende la solución de un sistema dinámico a una vecindad completa de condiciones iniciales en lugar de limitarse a una sola trayectoria. Al representar la solución como una serie de Taylor multivariable, podemos capturar cómo las trayectorias del sistema cambian en respuesta a pequeñas perturbaciones en las condiciones iniciales o parámetros, lo que permite estudiar la estabilidad y sensibilidad del sistema.

Implementación en Julia

Regresamos a nuestra definición de nuestras ecuaciones en odnde ahora du[5] = zero(μ) tiene más sentido, ya que vamos a hacer Jet Transport, pero no vamos a variar las condiciones iniciales, sino el parámetro de masa.

@taylorize function three_body_restricted_param!(du::Vector{T}, u::Vector{T}, p, t) where T
    x, y, v_x, v_y, μ = u

    x_plus_mu = x + μ
    x_minus_one_plus_mu = x - 1 + μ
    one_minus_mu = 1 - μ  

    r1 = sqrt(x_plus_mu^2 + y^2)
    r2 = sqrt(x_minus_one_plus_mu^2 + y^2)

    r1_cubed = r1^3
    r2_cubed = r2^3

    du[1] = v_x
    du[2] = v_y
    du[3] = (2v_y + x) - (one_minus_mu * x_plus_mu / r1_cubed + μ * x_minus_one_plus_mu / r2_cubed)
    du[4] = (-2v_x + y) - (one_minus_mu * y / r1_cubed + μ * y / r2_cubed)
    du[5] = zero(μ)
end

Explicación de las Ecuaciones

Estas ecuaciones de movimiento representan un sistema de tres cuerpos en el que una de las masas es significativamente menor que las otras dos (problema de tres cuerpos restringido). La función three_body_restricted_param! define cómo evoluciona el sistema con el tiempo, y el uso de @taylorize permite calcular automáticamente las derivadas necesarias para el Jet Transport.

Configuración Inicial

varorder = 6
ξ = set_variables("ξ", numvars=5, order=varorder)
q0TN = [x0, y0, vx0, vy0, μ0] .+ [0*ξ[1], 0*ξ[2], 0*ξ[3], 0*ξ[4], ξ[5]]

Aquí, como se estudió en la entrada mencionada al principio, el uso de ξ permite representar las desviaciones de las condiciones, esenciales para el Jet Transport. q0TN es el vector de condiciones iniciales con componentes polinómicas que representan la variación de μ.

Integración con Jet Transport

result = taylorinteg(three_body_restricted_param!, q0TN, time_vector, order, abstol, maxsteps=900000)
result.x

La función taylorinteg realiza la integración numérica del sistema, proporcionando una solución que no solo representa la evolución de las variables del sistema sino también su dependencia en relación con μ y otras perturbaciones iniciales.

Análisis y Visualización

δμ_values = LinRange(0, 0.0017995, 30)
μ_values = μ0 .+ δμ_values
num_times = length(time_vector)
num_μ = length(μ_values)

xjet_plot2 = zeros(num_times, num_μ)
vjet_plot2 = zeros(num_times, num_μ)

for i in 1:num_times
    for j in 1:num_μ
        μ = μ_values[j]
        ξ_values = [0.0, 0.0, 0.0, 0.0, μ - μ0]  # μ - μ0 porque ξ[5] representa la desviación de μ0
        xjet_plot2[i, j] = result.x[i,1](ξ_values)
        vjet_plot2[i, j] = result.x[i,2](ξ_values)
    end
end

Aquí se calcula las trayectorias para diferentes valores de μ, basándose en la solución obtenida mediante Jet Transport. Las trayectorias se representan en matrices xjet_plot2 y vjet_plot2.

Visualización de Resultados

plotly()
p = plot(legend=:outertopleft, alpha=1.0)
for j in 1:num_μ
    plot!(xjet_plot2[:, j], vjet_plot2[:, j], label="μ = $(round(μ_values[j], digits=5))")
end
display(p)

Como podemos ver, tenemos una serie de trayectorias que parece que de alguna forma van divergiendo.

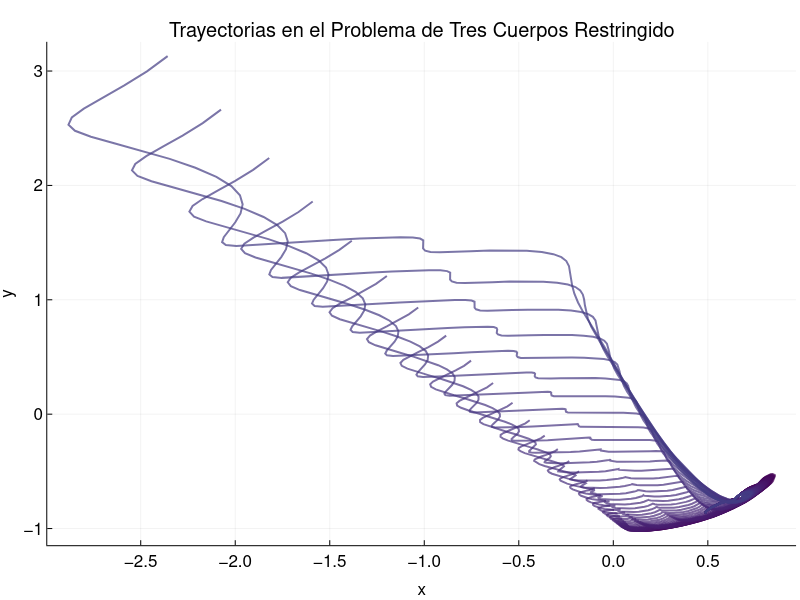
Acerquémonos un poco más a la región en donde parece que todo estaba bien.

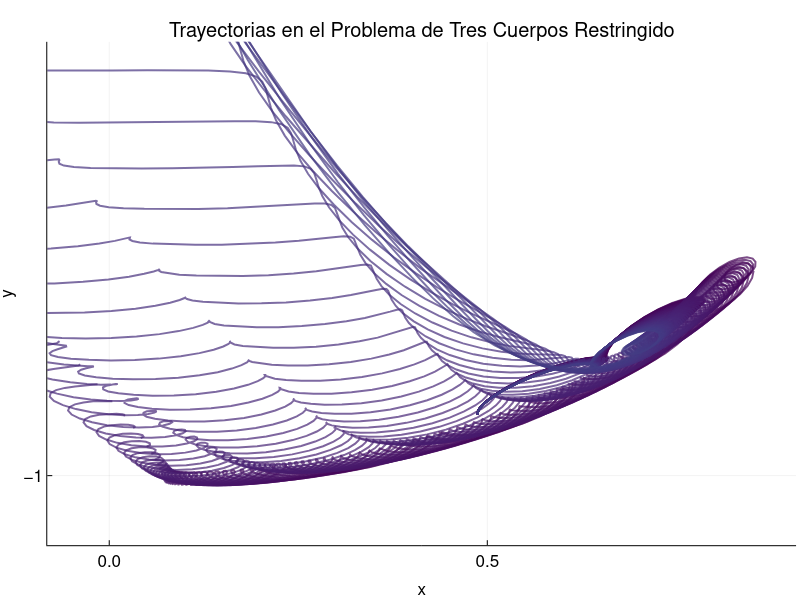
Un poco más.

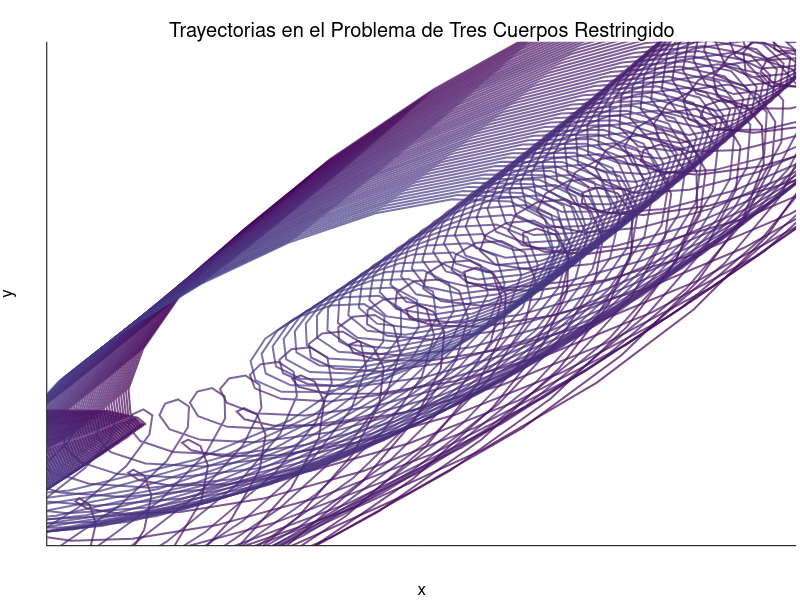
De esta forma no es tan práctico observar cómo es que las trayectorias van divergiendo conforme vamos cambiando el parámetro de masa, pero en la siguiente animación se ve un poco más claro de qué es lo que está pasando.

anim = @animate for j in 1:num_μ
    plot(legend=:outertopleft, alpha=1.0)
    plot!(xjet_plot2[:, j], vjet_plot2[:, j], 
          label="μ = $(round(μ_values[j], digits=5))",
          xlabel="x", ylabel="v")
    title!("μ = $(round(μ_values[j], digits=5))")
end

# Guardar la animación como un gif
gif(anim, "trayectorias.gif", fps=7)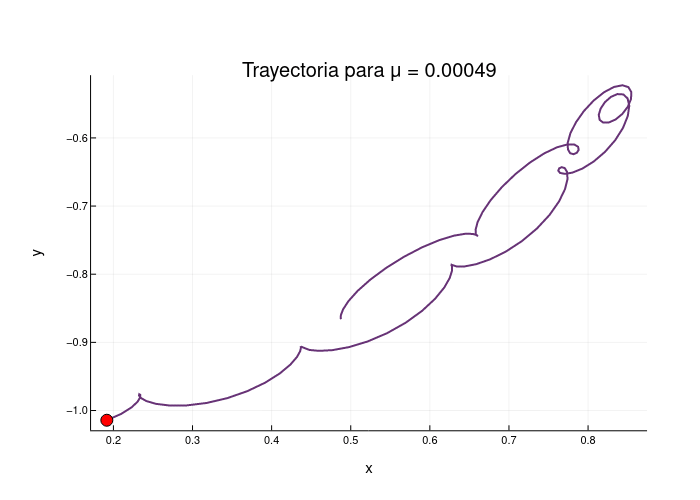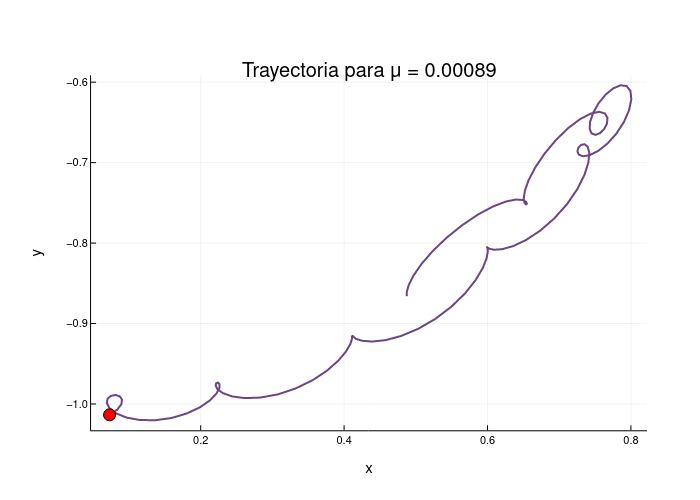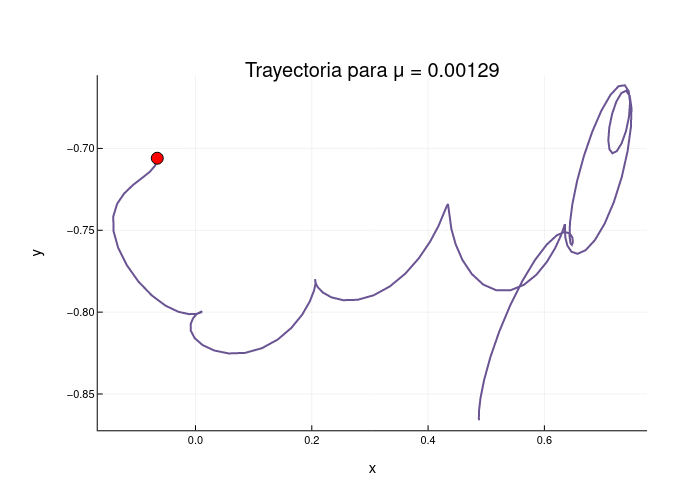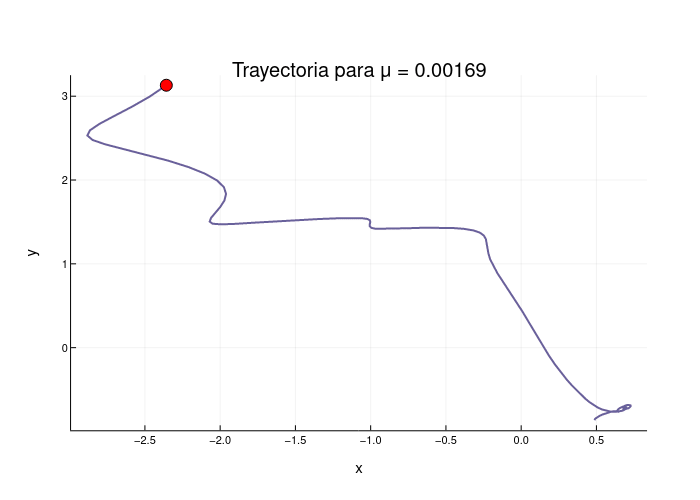

La animación creada muestra la evolución de las trayectorias a medida que μ varía, el punto rojo muestra el final de la trayectoria para el tiempo especificado, esto es el comportamiento del sistema cerca de L5.

Por lo tanto, el uso de Jet Transport en combinación con TaylorIntegration.jl permite no solo resolver las ecuaciones de movimiento de un sistema complejo como el problema de tres cuerpos, sino también explorar cómo las variaciones en las condiciones iniciales y los parámetros afectan el comportamiento del sistema.