❉ Solución Numérica al Problema de Tres Cuerpos ❉

Ya que quedaron las condiciones iniciales, ahora podemos dar el siguiente paso: resolver utilizando la paquetería TaylorIntegration.jl de Julia para resolver el problema de tres cuerpos restringido, específicamente cerca de uno de los puntos de Lagrange que ya obtuvimos.

Introducción a la Solución Numérica

Se estudió que el problema de tres cuerpos describe el movimiento de tres masas bajo su mutua atracción gravitacional. Aunque existen soluciones analíticas para casos específicos, la mayoría de las configuraciones requieren métodos numéricos para obtener soluciones aproximadas. En este contexto, utilizaremos el método de Taylor, implementado en Julia mediante la paquetería TaylorIntegration.jl, para integrar las ecuaciones de movimiento del sistema.

La implementación de las ecuaciones de movimiento ya la vimos:

@taylorize function three_body_restricted_param!(du::Vector{T}, u::Vector{T}, p, t) where T
    x, y, v_x, v_y, μ = u

    x_plus_mu = x + μ
    x_minus_one_plus_mu = x - 1 + μ
    one_minus_mu = 1 - μ  

    r1 = sqrt(x_plus_mu^2 + y^2)
    r2 = sqrt(x_minus_one_plus_mu^2 + y^2)

    r1_cubed = r1^3
    r2_cubed = r2^3

    du[1] = v_x
    du[2] = v_y
    du[3] = (2v_y + x) - (one_minus_mu * x_plus_mu / r1_cubed + μ * x_minus_one_plus_mu / r2_cubed)
    du[4] = (-2v_x + y) - (one_minus_mu * y / r1_cubed + μ * y / r2_cubed)
    du[5] = zero(μ)
end

# Configuración inicial
x0, y0, vx0, vy0  = 0.48765, -0.86602, 0.0, 0.0
μ0 = 0.01234/25 # μ cerca de L5
initial_conditions2 = [x0, y0, vx0, vy0, μ0]
t0 = 0.0
tend = 600.0
step = 0.1
time_vector = t0:step:tend
order = 20
abstol = 1e-20
d2 = taylorinteg(three_body_restricted_param!, initial_conditions2, time_vector, order, abstol; maxsteps=90000)
plot(d2.x[:,1], d2.x[:,2], label="", color=:black, alpha=0.5)

• Condiciones Iniciales:

  • x0, y0: Posición inicial cerca del punto de Lagrange L5.

  • vx0, vy0: Velocidades iniciales, en este caso, ambas cero para simular una pequeña perturbación alrededor de L5.

• Parámetros de Integración:

  • t0: Tiempo inicial.

  • tend: Tiempo final para la simulación.

  • step: Paso de tiempo para la generación del vector de tiempo.

  • time_vector: Vector de tiempo desde t0 hasta tend con incrementos de step.

  • order: Orden del método de Taylor. Un orden más alto puede proporcionar mayor precisión.

  • abstol: Tolerancia absoluta para el método de integración, determinando la precisión deseada.

3. Integración Numérica

d2 = taylorinteg(three_body_restricted_param!, initial_conditions2, time_vector, order, abstol; maxsteps=90000)

Explicación:

• Función taylorinteg: Ejecuta la integración numérica utilizando el método de Taylor, basado en las derivadas definidas en three_body_restricted_param!.

• Parámetros:

  • three_body_restricted_param!: La función que define las ecuaciones de movimiento.

  • initial_conditions2: Vector de condiciones iniciales.

  • time_vector: Vector de tiempo para la simulación.

  • order: Orden del método de Taylor.

  • abstol: Tolerancia absoluta.

  • maxsteps=90000: Número máximo de pasos de integración permitidos para evitar bucles infinitos en caso de que la integración no converja.

4. Visualización de los Resultados

plot(d2.x[:,1], d2.x[:,2], label="", color=:black, alpha=0.5)

Lo que estamos viendo es la trayectoria del tercer cuerpo visto desde el marco de referencia no inercial.

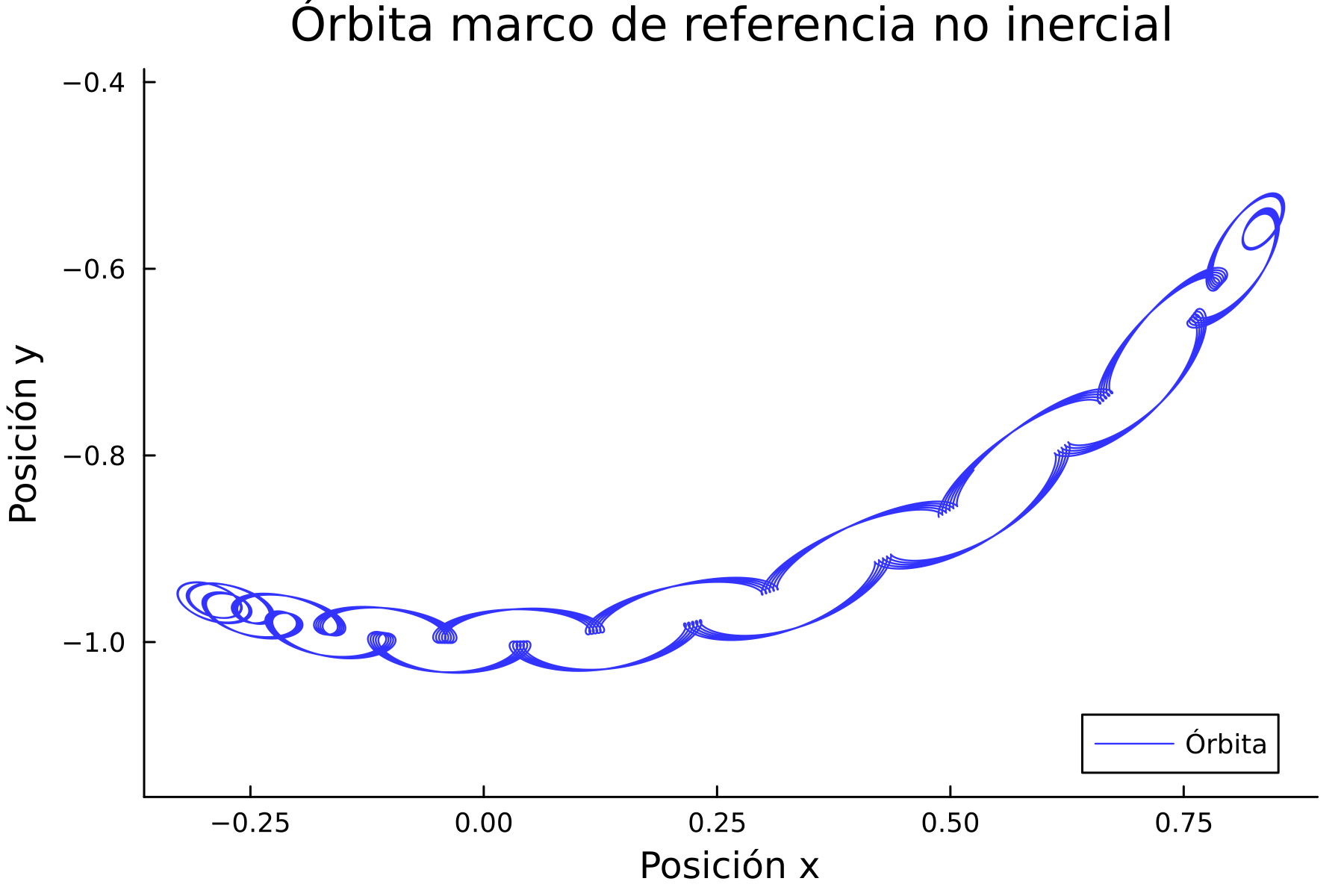
Podemos observar que si hacemos la transformación al sistema de referencia inercial, ya vemos algo más familiar.

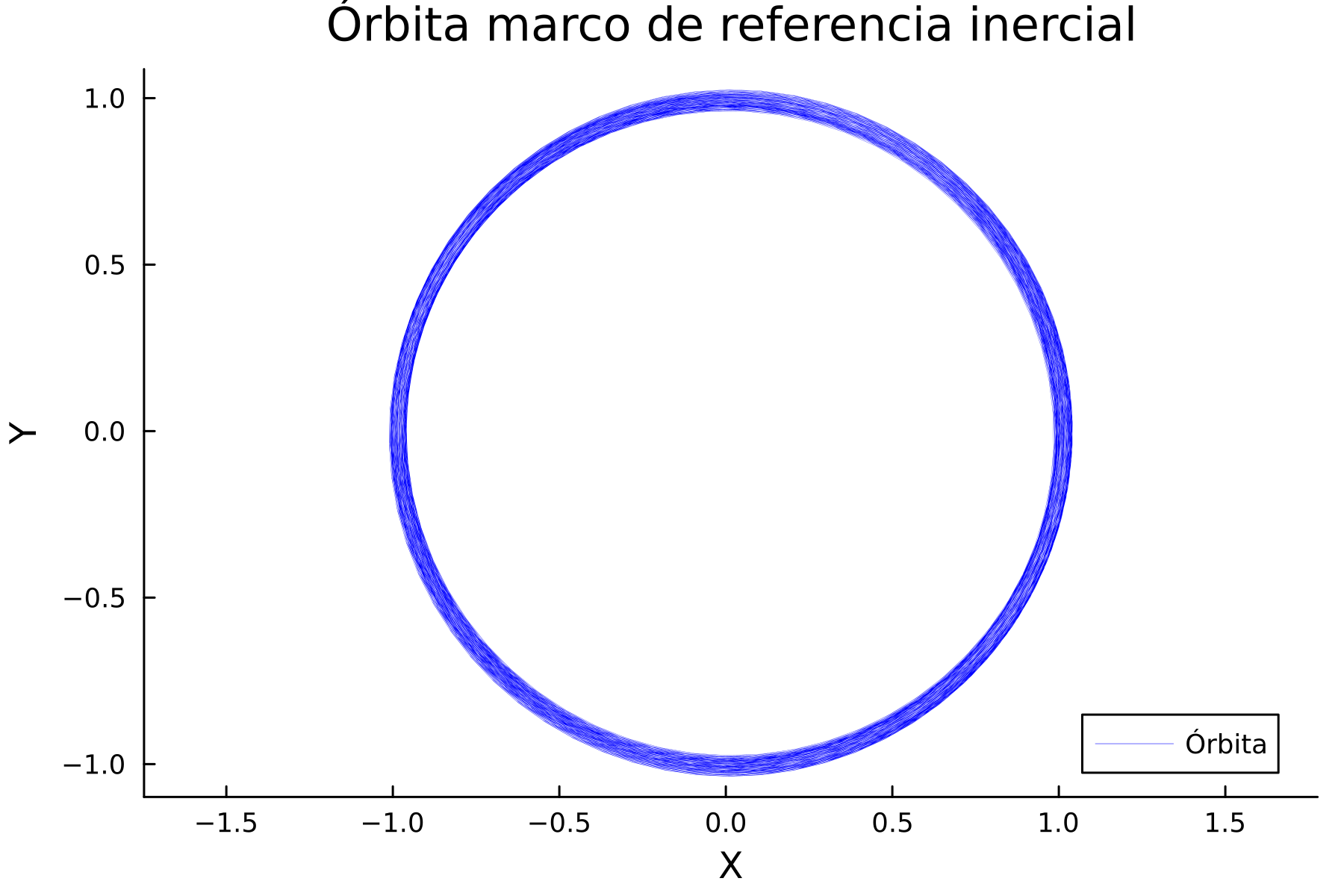
En nuestros resultados podemos observar algunas cosas interesantes:

1. En el punto $L_5$, aunque es un punto de equilibrio estable, las perturbaciones pueden generar movimientos complejos. Pequeñas perturbaciones en la posición o velocidad de un objeto pueden producir trayectorias en espiral o movimientos irregulares debido a la naturaleza de la atracción gravitacional de los otros dos cuerpos (por ejemplo, el Sol y la Tierra o un sistema similar).

2. En un marco de referencia no inercial, como el que se usa para representar nuestra dinámica cerca de $L_5$, aparecen fuerzas ficticias como la de Coriolis. Estas fuerzas pueden hacer que la trayectoria del objeto tenga curvas y giros complejos en lugar de seguir un camino suave.

3. Cualquier pequeña fuerza externa, como la atracción gravitacional de otros cuerpos cercanos, podría hacer que la órbita de un objeto alrededor de $L_5$ sea inestable o tome formas inesperadas.

4. Las órbitas cercanas a $L_5$ pueden tomar formas complicadas, conocidas como órbitas de libración. Estas órbitas pueden oscilar alrededor de $L_5$ y tener trayectorias en bucle o en forma de "8" debido a la influencia combinada de las fuerzas gravitacionales de los dos cuerpos primarios y la rotación del sistema.